A point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
23
13
34
14
The correct Answer is:C
To solve the problem of finding the probability that a point selected at random from inside a circle is closer to the circumference than to its center, we can follow these steps:
1. Understand the Problem: We need to determine the area inside the circle where points are closer to the circumference than to the center.
2. Draw the Circle: Let’s consider a circle with radius r. The center of the circle is denoted as point O.
3. Identify the Condition: A point P inside the circle is closer to the circumference than to the center if the distance from P to the circumference is less than the distance from P to the center O.
4. Set up the Relationship: The distance from point P to the center O is OP, and the distance from P to the circumference is r−OP. We need to find when:
r−OP<OP
Simplifying this gives:
r<2⋅OP⇒OP>r2
5. Define the Inner Circle: The points that are closer to the center than to the circumference are those within a smaller circle of radius r2 centered at O.
6. Calculate Areas:
- Total Area of the Larger Circle:
Atotal=πr2
- Area of the Smaller Circle (where points are closer to the center):
Ainner=π(r2)2=πr24
7. Area Where Points are Closer to the Circumference:
Aevent=Atotal−Ainner=πr2−πr24=πr2(1−14)=πr2⋅34=3πr24
8. Calculate the Probability:
The probability P that a randomly selected point is closer to the circumference than to the center is given by the ratio of the area where this condition holds to the total area:
P=AeventAtotal=3πr24πr2=34
Final Answer:
The probability that a point selected at random from inside the circle is closer to the circumference than to its center is 34.
---
r−OP<OP
Simplifying this gives:
r<2⋅OP⇒OP>r2
- Total Area of the Larger Circle:
Atotal=πr2
- Area of the Smaller Circle (where points are closer to the center):
Ainner=π(r2)2=πr24
Aevent=Atotal−Ainner=πr2−πr24=πr2(1−14)=πr2⋅34=3πr24
The probability P that a randomly selected point is closer to the circumference than to the center is given by the ratio of the area where this condition holds to the total area:
P=AeventAtotal=3πr24πr2=34
The probability that a point selected at random from inside the circle is closer to the circumference than to its center is 34.
Topper's Solved these Questions
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - B Objective Type Questions (One option is correct))
64 Videos
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - C Objective Type Questions (More than one options are correct))
21 Videos
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - TRY YOURSELF
42 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions
8 Videos
Similar Questions
Knowledge Check
If the circumference of a circle is 110 cm , find its radius .
A19.5 cm.B17.5 cm.C18.5 cm.D15.5 cm.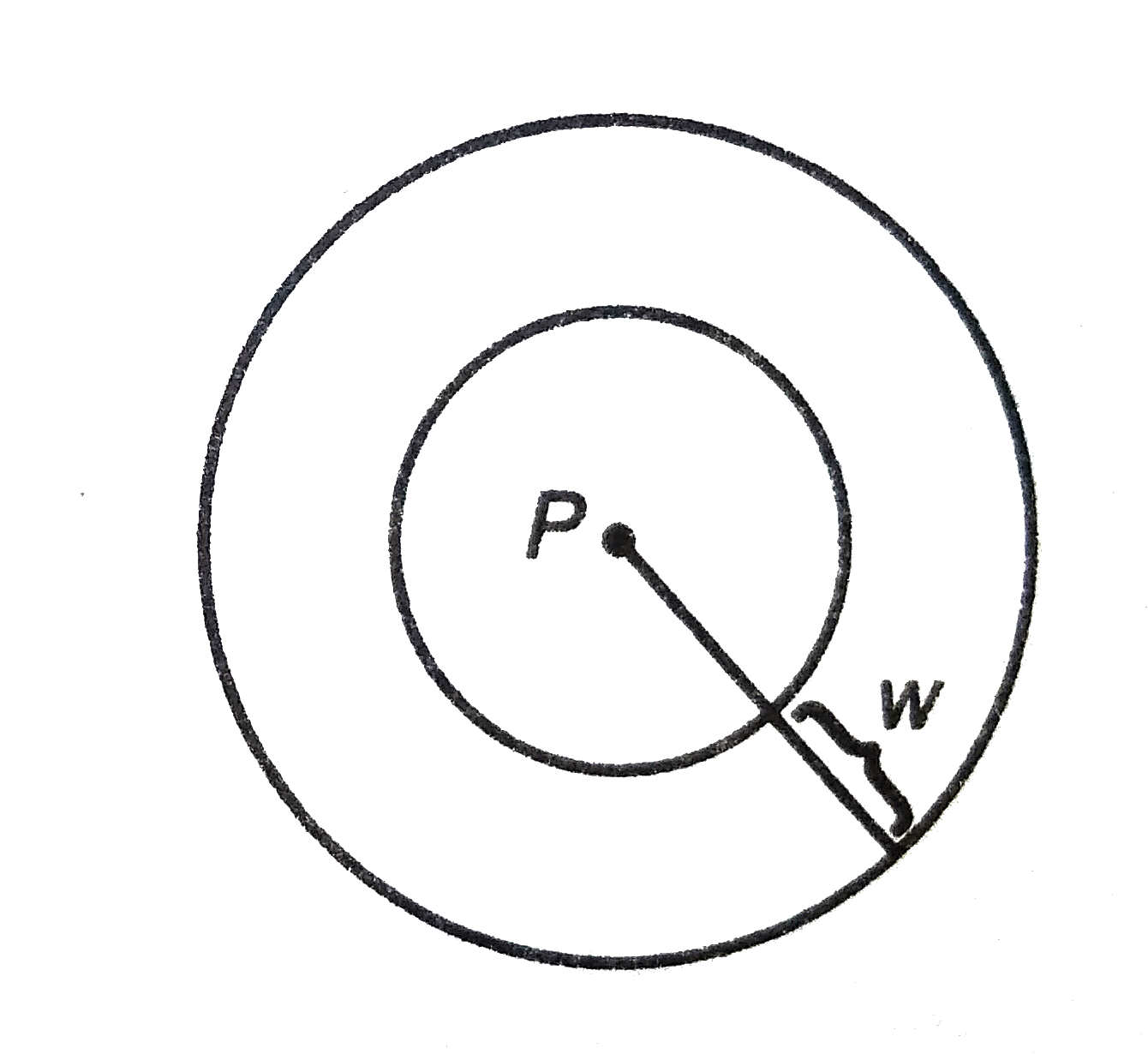
In the figure above, point P is the center of each circle. The circumference of the larger circle exceeds the circumference of the smaller circle by 12π. What is the width, w, of the region between the two circles?A4B6C8D9
Three points P,QandR are selected at random from the cirumference of a circle. Find the probability p that the point lie on a semi-circle
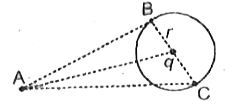
View SolutionA point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
View SolutionOut of two unequal chords of a circle, the bigger chord is closer to the centre of the circle. Prove it.
View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
View SolutionIf two points are taken at random on the circumference of circle, the chance that their distance apart is greater than the radius of the circle is
View SolutionShow that the points (-3, 2), (2, -3) and (1, 2√3) lie on the circumference of that circle, whose centre is origin.
View Solution
