The locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0,(1+q)x−qy+q(1+q)=0 and y = 0, where p≠⋅q, is (A) a hyperbola (B) a parabola (C) an ellipse (D) a straight line
hyperbola
a parabola
an ellipse
a straight line
The correct Answer is:D
The equations of the sides of the triangle are :
L1≡xp−y1+p=−1,L2≡xq=y1+q=−1,L3≡y=0
The coordinates of vertices are A(−p,0),B(−q,0)andC(pq,(1+p)(1+q)).
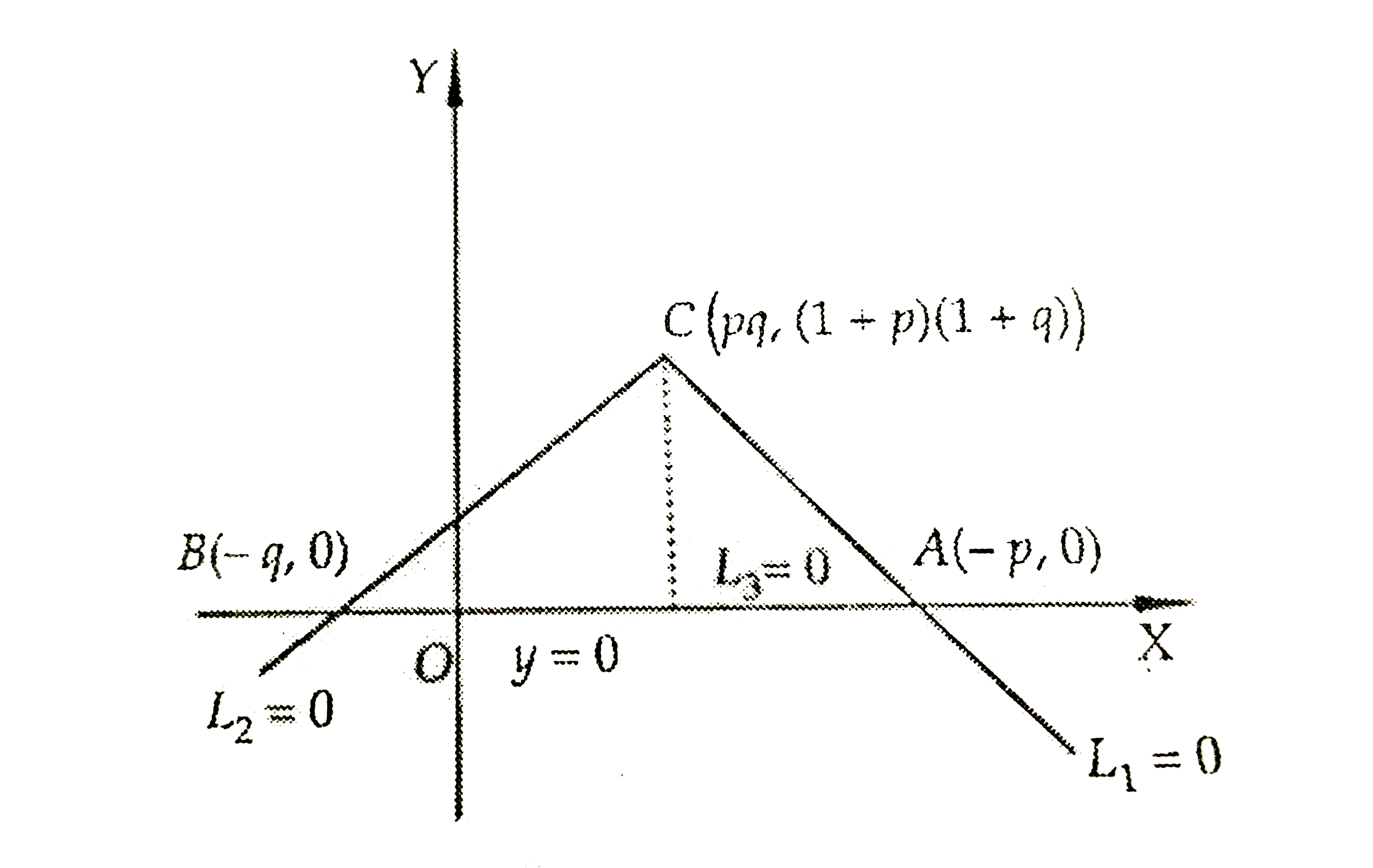
The equation of the altitude through C is x = pq and the equation of the altitude through B is (1+p) y + px + pq = 0.
Solving these equations , we get x = pq , y = -pq
Let (h,k) be the coordinates of the orthocentre . Then ,
h = pq and k = -pq ⇒ k = - h
Hence , the locus of (h,k) is y = -x , which is a straight line .
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
The locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0.,(1+q)x−qy+q(1+q)=0 andy=0wherept (a) a hyperbola (c) an ellipse (b) a parabola (d) a straight line
View SolutionIf a+b+3c=0,c≠0andpandq be the number of real roots of the equation ax2+bx+c=0 belonging to the set (0,1) and not belonging to set (0,1) respectively, then locus of the point of intersection of lines xcosθ+ysinθ=p and xsinθ−ycosθ=q, where θ is a parameter is : (A) a circle of radius √2 (B) a straight line (C) a parabola (D) a circle of radius 2
View Solution
Knowledge Check
The point of injtersection of the line xp+yq=1andxq+yp=1 lies on the line
Ax−y=0B(x+y)(p+q)=2qpC(ax+by)(p+q)=(a+b)pqD(ax−by)(p+q)=)a−b)pqThe value of 1.999….. In the form of pq, where p and q are integers and q≠0, is
A1910B19991000C2D19
Show that the reflection of the line px+qy+r=0 in the line x+y+1=0 is the line qx+py+(p+q−r)=0, where p≠−q.
View SolutionThe curve represented by the equation √px+√qy=1 where p,q∈R,p,q>0, is a circle (b) a parabola an ellipse (d) a hyperbola
View SolutionThe equations of the tangents drawn from the origin to the circle x2+y2−2px−2qy+q2=0 are perpendicular if (A) p2=q2 (B) p2=q2=1 (C) p=q2 (D) q=p2
View SolutionIf the lines p1x+q1y=1,p2x+q2y=1andp3x+q3y=1 be concurrent, show that the points (p1,q1),(p2,q2)and(p3,q3) are colliner.
View SolutionIf Q(h,k) is the foot of the perpendicular from P(x1,y1) on the line ax+by+c=0 then Q(h,k) is
View SolutionSolve for x and y, px + qy = 1 and qx+py=(p−q)2p2+q2−1.
View Solution
