The locus of the point which divides the double ordinates of the ellipse in the ratio internally is Solution in Tamil
none of these
The correct Answer is:A
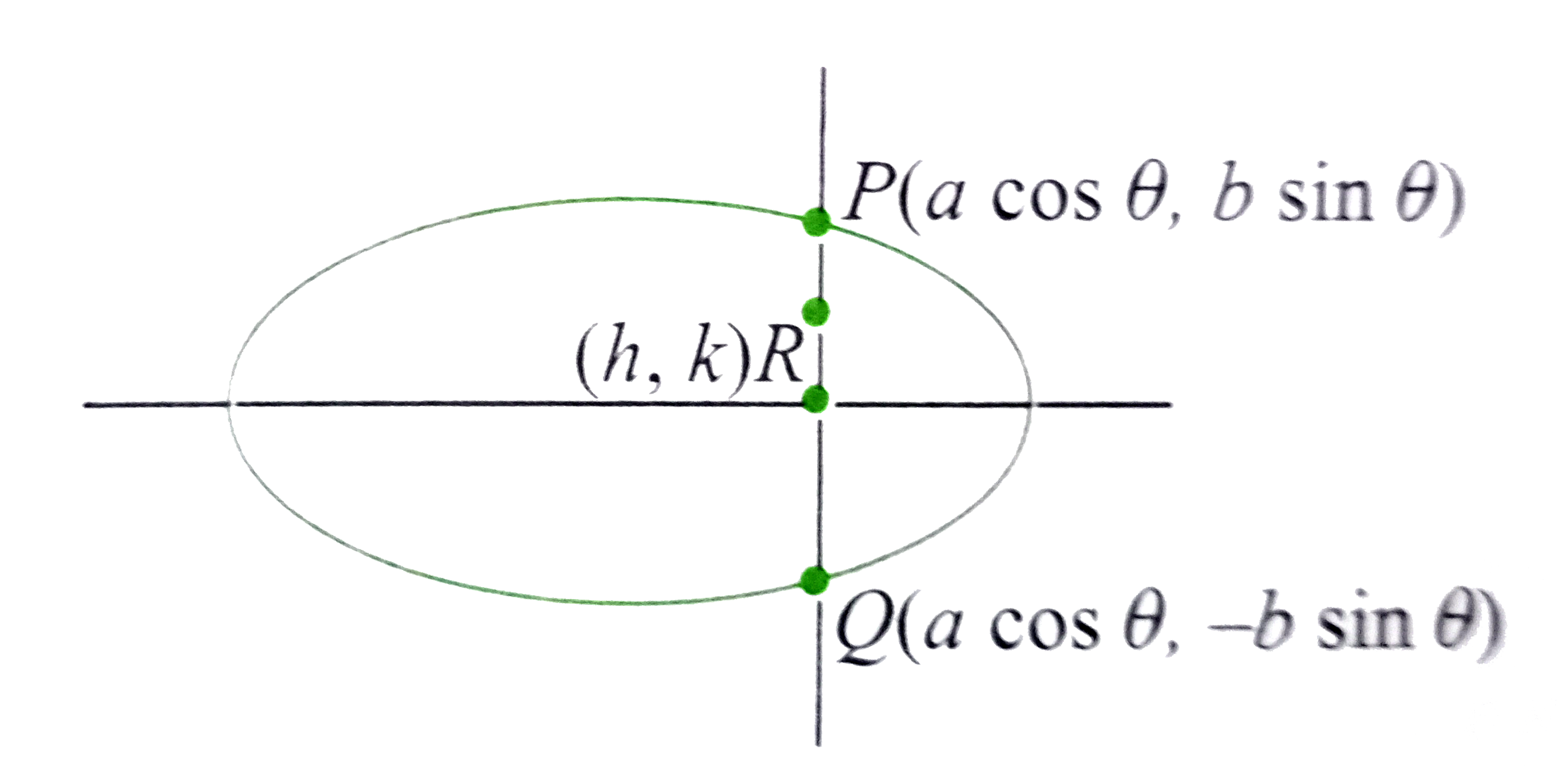
Let
or
or
or
On squaring and adding (1) and (2), we get
Similar Questions
The locus of a point which divides the line segment joining the point (0, -1) and a point on the parabola,x2=4y internally in the ratio 1: 2, is:
View SolutionThe locus of the point which divides the double ordinates of the ellipse x2a2+y2b2=1 in the ratio 1:2 internally is
View SolutionThe co-ordinates of the point which divides the line joining (1, -2) and (4, 7) internally in the ratio 1 : 2 are
View SolutionThe co-ordinates of a point (x, y) which divides the straight line joining two points (x1,y1) and (x2,y2) internally in the ratio m1 and m2 are
View SolutionFind the locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 at the points the sum of whose ordinates are constant.
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 which meet at right , is
View SolutionFind the co-ordinates of the point which divides the line joining (5,-2) and (9,6) internally in the ratio 1:2.
View SolutionThe locus of the point which divides the double ordinates of the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 in the ratio 1:2 internally is (x^2)/(a^2)+(9y^2)/(b^2)=1 (b) (x^2)/(a^2)+(9y^2)/(b^2)=1/9 (9x^2)/(a^2)+(9y^2)/(b^2)=1 (d) none of these
View Solution
