A=(2,−1) locus of B is x2+y2=25. If P divides AB in the ratio 1:2 then locus of P is
Step by step video & image solution for A=(2,-1) locus of B is x^2+y^2=25. If P divides AB in the ratio 1:2 then locus of P is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let P be a point on x2=4y. The segment joining A(0,−1) and P is divided by point Q in the ratio 1:2, then locus of point Q is
A9x2=3y+2B9x2=12y+8C9y2=12x+8D9y2=3x+2A variable line through the point (65,65) cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio 2:1, then the equation of the locus of P is
A5xy=(2x+y)B5xy=2(2x+y)C5xy=(x+2y)D5xy=2(x+2y)If the foci of the ellipse x29+y2=1 student a right angle at a point P. Then, the locus of P is
Ax2+y2=1Bx2+y2=2Cx2+y2=4Dx2+y2=8
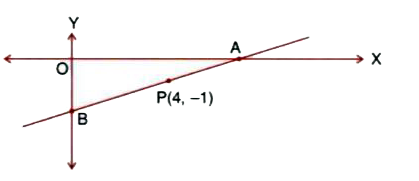
A line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.

Find the co-ordinates of A and B.
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.
Find the Coordinates of A and B
View SolutionA variable line through the point (65,65) cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio 2:1, then the equation of the locus of P is
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(i) Find the coordinates of A and B.
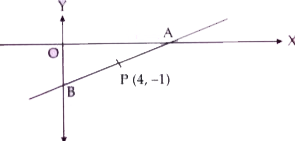
View SolutionA variable line through the point (65,65) cuts the coordinates axes in the point AandB. If the point P divides AB internally in the ratio 2:1, show that the equation to the locus of P is :
View Solution
