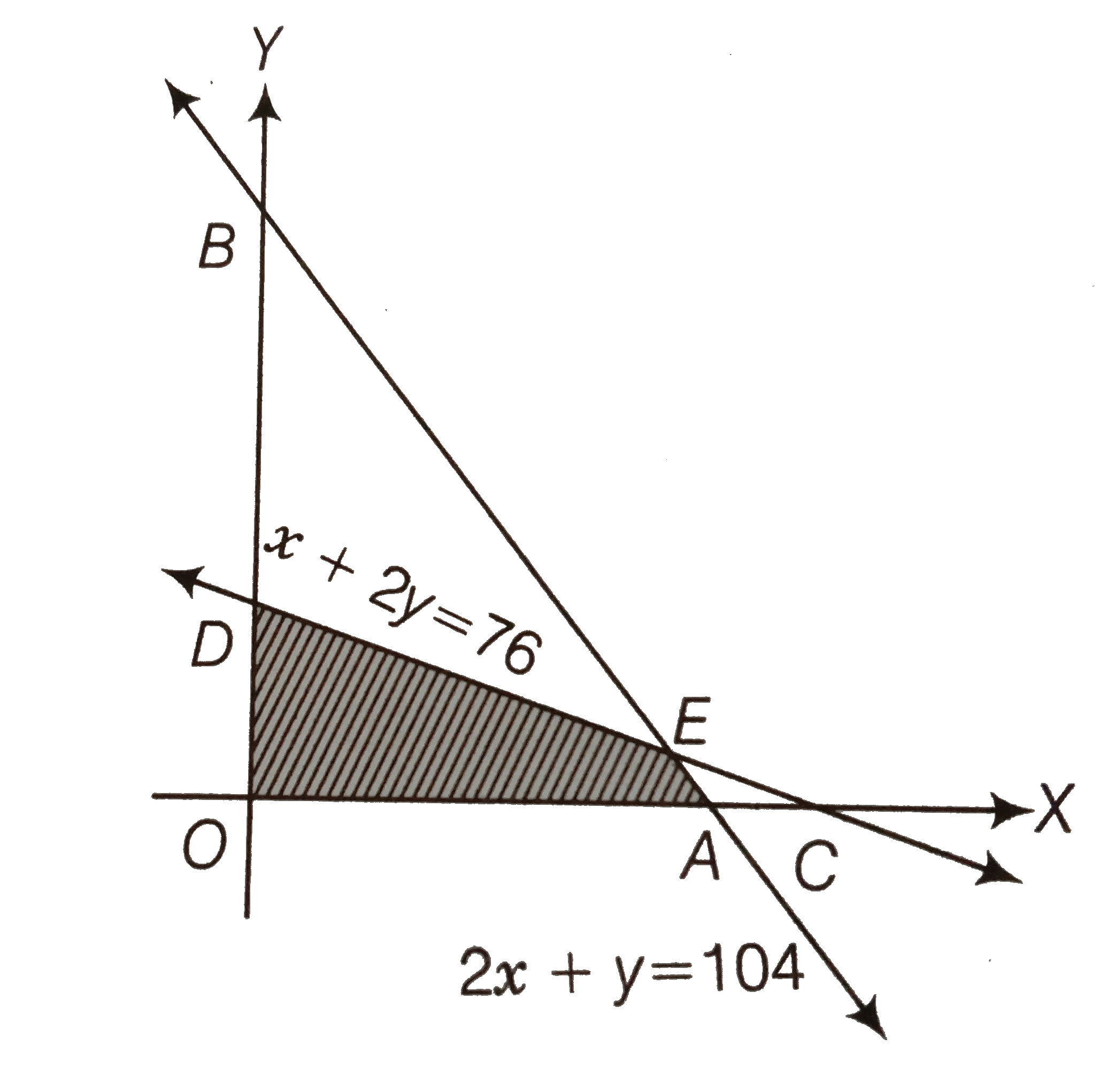
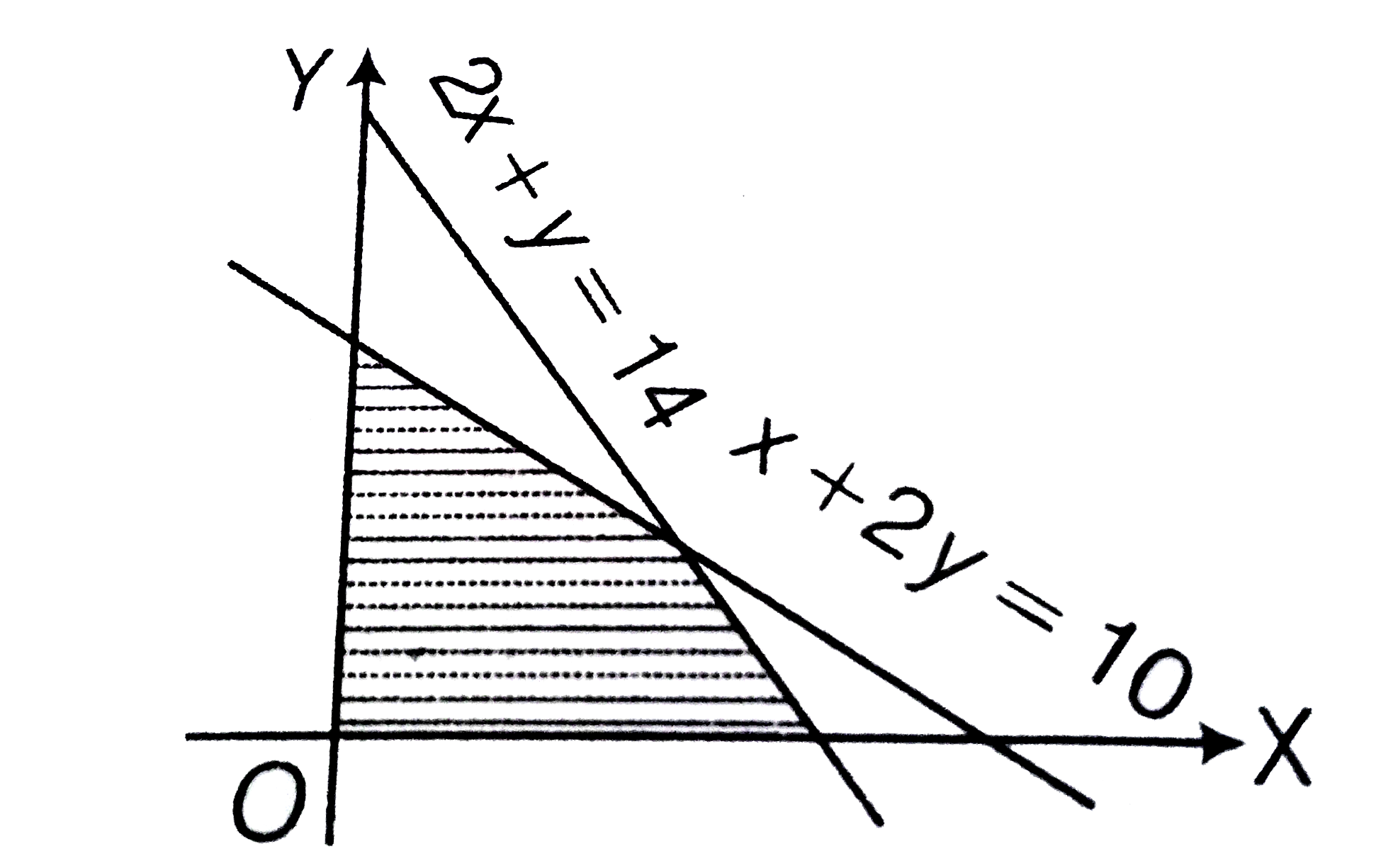
The maximum value of Z = 4x + 3y, if the feasible region for an LPP is shown in following figure, is

A

112

B

100

C

72

D

110

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The feasible region is bounded. Therefore,maximum of Z must occurs at the corner points of the feasible region.

Hence, the maximum vlaue of Z is 112 .

|

Updated on:21/07/2023

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30videos
Linear Programming
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13videos
Linear Programming
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13videos
Linear Programming
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3videos
LINE
BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22videos
MATHEMATICAL LOGIC

Similar Questions

Knowledge Check

Question 1 - Select One
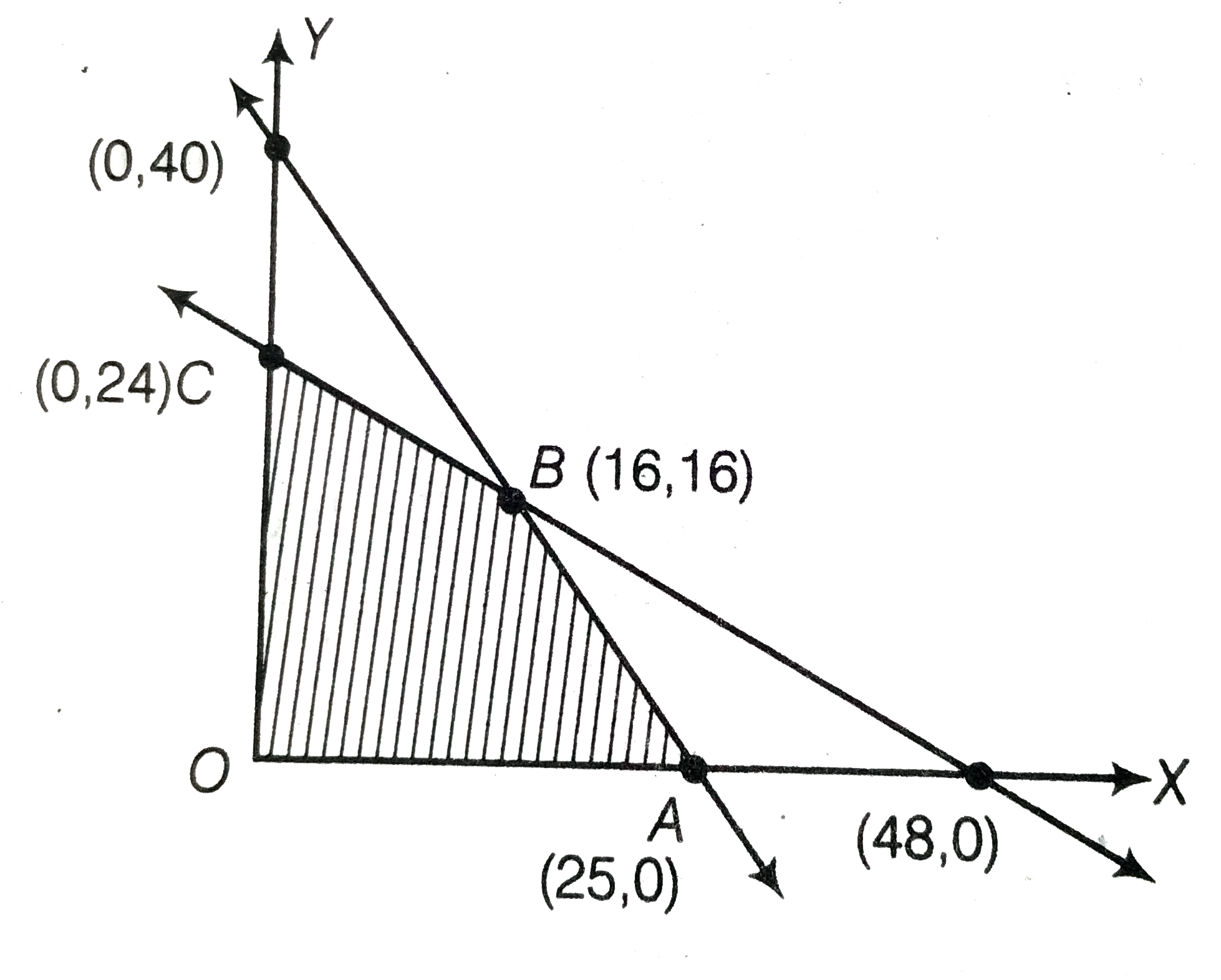
Determine the minimum value of $Z = 3 x + 2 y$ (if any), if the feasible region for an LPP is shown in figure:

AMinimum value of Z = 11.
BMinimum value of Z = 14.
CMinimum value of Z = 12.
DMinimum value of Z = 13.
Question 2 - Select One
The feasible region for an LPP is shown in following figure. Find the minimum value of $Z = 11 x + 7 y .$

A $22$
B $23$
C $24$
D $21$
Question 3 - Select One
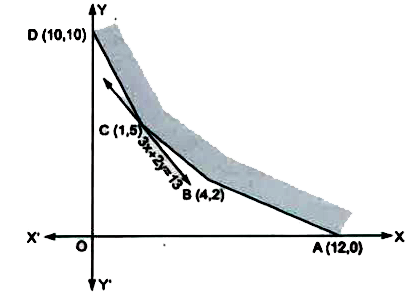
The feasible region for an $L P P$ is shown in the following figure. Let $F = 3 x - 4 y$ be the objective function. Maximum value of $F$ is

A $0$
B $8$
C $12$
D $- 18$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-Linear Programming -EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )

Home
Ask Doubt
Profile