The mean of the distribution, in which the values of X are 1, 2, ..,n the frequency of each being unity is :
n(n+1)2
n2
n+12
none of these
The correct Answer is:C
To find the mean of the distribution where the values of X are 1,2,…,n and the frequency of each value is unity, we can follow these steps:
1. Identify the Values and Frequencies:
- The values of X are x1=1,x2=2,…,xn=n.
- The frequency fi for each xi is 1 (unity).
2. Calculate the Product of Values and Frequencies:
- We need to calculate xi⋅fi for each i:
- x1⋅f1=1⋅1=1
- x2⋅f2=2⋅1=2
- x3⋅f3=3⋅1=3
- ...
- xn⋅fn=n⋅1=n
3. Sum of the Products:
- Now, we sum these products:
n∑i=1xifi=1+2+3+…+n
4. Use the Formula for the Sum of First n Natural Numbers:
- The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
- Therefore, we can write:
n∑i=1xifi=n(n+1)2
5. Calculate the Mean:
- The mean ¯x is calculated using the formula:
¯x=∑ni=1xifi∑ni=1fi
- Since the frequency of each value is 1, the total number of values (or total frequency) is n:
n∑i=1fi=n
- Thus, the mean becomes:
¯x=n(n+1)2n=n+12
Final Result:
The mean of the distribution is:
¯x=n+12
- The values of X are x1=1,x2=2,…,xn=n.
- The frequency fi for each xi is 1 (unity).
- We need to calculate xi⋅fi for each i:
- x1⋅f1=1⋅1=1
- x2⋅f2=2⋅1=2
- x3⋅f3=3⋅1=3
- ...
- xn⋅fn=n⋅1=n
- Now, we sum these products:
n∑i=1xifi=1+2+3+…+n
- The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
- Therefore, we can write:
n∑i=1xifi=n(n+1)2
- The mean ¯x is calculated using the formula:
¯x=∑ni=1xifi∑ni=1fi
- Since the frequency of each value is 1, the total number of values (or total frequency) is n:
n∑i=1fi=n
- Thus, the mean becomes:
¯x=n(n+1)2n=n+12
The mean of the distribution is:
¯x=n+12
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Section I - Solved Mcqs24videos
MEASURES OF CENTRAL TENDENCY
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test29videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test29videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
Similar Questions
The mean of the distribution is 50.

Find the value of a and hence the frequencies of 30 and 70.View SolutionIf the mean of the following distribution is 3 find the value of p.
 View Solution
View SolutionIf the mean of the following distribution is 6, find the value of p
View SolutionIf the mean of the following distribution is 24, find the value of 'a'.
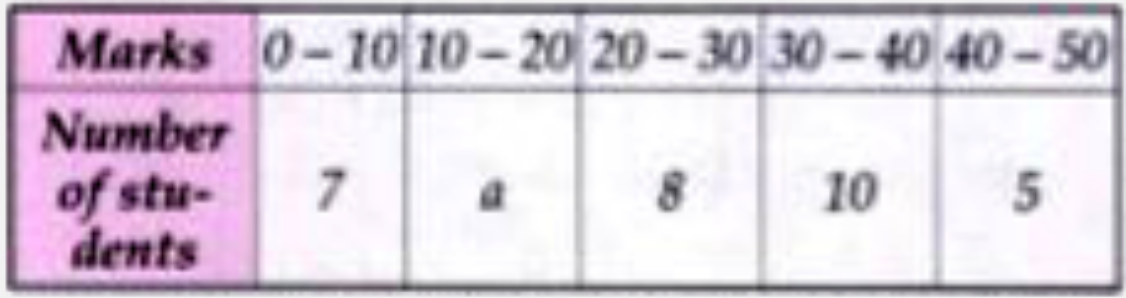 View Solution
View SolutionIf the mean of the following distribution is 2.6 Then the value of p is
Variable x: 1 2 3 4 5
frequency of x: 4 5 P 1 2View SolutionMedian of a distribution is the value of the variable which divides it into equal parts . In case of individual observations x1,x2 .. xn, if the number of observations is odd, then median is the value of (n+12) th observation when the observations have been arranged in ascending or descending order of magnitude. In case of even number of observations median is the A.M. of the values of (n2)th and (n2+1) th observations, arranged in ascending or descending order of magnitude . The mode of distribution is that value of the variable for which the frequency is maximum .
Median of the distribution 8,5,7,9,13,11,20,23 , 25 ,28 , 27 isView SolutionMedian of a distribution is the value of the variable which divides it into equal parts . In case of individual observations x1,x2 .. xn, if the number of observations is odd, then median is the value of (n+12) th observation when the observations have been arranged in ascending or descending order of magnitude. In case of even number of observations median is the A.M. of the values of (n2)th and (n2+1) th observations, arranged in ascending or descending order of magnitude . The mode of distribution is that value of the variable for which the frequency is maximum .
Median of the distribution 25,20,11,3,12,18,17 ,9,21,22 isView SolutionIf the mean of the distribution is 2.6, then the value of y is
Variate x12345Frequency f of x45y12View SolutionThe mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f1 and f2
 View Solution
View SolutionIf the mean of the following distribution is 2.6, then the value of y is Variable (x) : 1 2 3 4 5 Frequency (y) : 4 5 y 1 2 (a) 3 (b) 8 (c) 13 (d) 24
View Solution

