If 3x+22x≥5x, then the solution set for x, is
(−∞,2]
[2,∞)
[0,2]
{2}
The correct Answer is:A
To solve the inequality 3x+22x≥5x, we will follow these steps:
Step 1: Rewrite the inequality
We start with the given inequality:
3x+22x≥5x
We can rewrite 22x as (2x)2:
3x+(2x)2≥5x
Step 2: Substitute y=2x
Let y=2x. Then 3x=(32)xy and 5x=(52)xy. The inequality becomes:
(32)xy+y2≥(52)xy
Step 3: Rearranging the inequality
Rearranging gives us:
y2+(32)xy−(52)xy≥0
Factoring out y:
y(y+(32)x−(52)x)≥0
Step 4: Analyzing the factors
1. The term y (which is 2x) is always positive for all real x.
2. We need to analyze the second factor:
y+(32)x−(52)x≥0
Step 5: Finding critical points
To find when the second factor is zero, we can set:
(32)x=(52)x
Taking logarithms gives:
xlog(32)=xlog(52)
This equality holds when x=0.
Step 6: Testing intervals
Now we will test intervals around the critical point x=2:
- For x<2: Choose x=1:
31+22⋅1=3+4=7and51=5⇒7≥5(True)
- For x=2:
32+22⋅2=9+16=25and52=25⇒25≥25(True)
- For x>2: Choose x=3:
33+22⋅3=27+64=91and53=125⇒91<125(False)
Conclusion
The inequality holds for x≤2. Therefore, the solution set is:
x∈(−∞,2)
We start with the given inequality:
3x+22x≥5x
We can rewrite 22x as (2x)2:
3x+(2x)2≥5x
Let y=2x. Then 3x=(32)xy and 5x=(52)xy. The inequality becomes:
(32)xy+y2≥(52)xy
Rearranging gives us:
y2+(32)xy−(52)xy≥0
Factoring out y:
y(y+(32)x−(52)x)≥0
1. The term y (which is 2x) is always positive for all real x.
2. We need to analyze the second factor:
y+(32)x−(52)x≥0
To find when the second factor is zero, we can set:
(32)x=(52)x
Taking logarithms gives:
xlog(32)=xlog(52)
This equality holds when x=0.
Now we will test intervals around the critical point x=2:
- For x<2: Choose x=1:
31+22⋅1=3+4=7and51=5⇒7≥5(True)
- For x=2:
32+22⋅2=9+16=25and52=25⇒25≥25(True)
- For x>2: Choose x=3:
33+22⋅3=27+64=91and53=125⇒91<125(False)
The inequality holds for x≤2. Therefore, the solution set is:
x∈(−∞,2)
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
If 1x−1≥2 , then the solution set is
AA. (1,32]BB. [1,32]CC. (1,32)DD. (−∞,−3]∪[12,∞)If 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
A B
B C
C D
D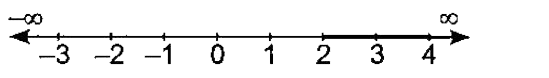
If x2−5≤x3−4,x∈R, then the solution set of x on the number line is:
A B
B C
C D
D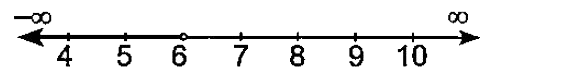
If (0.2)2x−3x−2>5 then complete solution set of values of x is
View SolutionIf 2x−5≤5x+4≤11 and x is a natural number (N), then the solution set of x is
View SolutionIf 2x−3≤x+1≤4x+7,x∈I (integers), then the solution set of x is
View SolutionIf −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
View SolutionIf 2x−5≤5x+4<29 and x is an integer, then the solution set of x is
View Solution
