The mean of the following data is 20.6. Find the value of p
To find the value of p given that the mean of the data is 20.6, we can follow these steps:
Step 1: Write down the given information
We know that the mean ¯x is given as 20.6. We also have the values of xi (the data points) and fi (the frequencies):
- xi=(10,15,p,25,35)
- fi=(3,10,25,7,5)
Step 2: Calculate ∑fi
We need to find the total frequency ∑fi:
∑fi=3+10+25+7+5=50
Step 3: Calculate ∑(xi⋅fi)
Next, we calculate ∑(xi⋅fi):
- For x1=10 and f1=3: 10⋅3=30
- For x2=15 and f2=10: 15⋅10=150
- For x3=p and f3=25: p⋅25=25p
- For x4=25 and f4=7: 25⋅7=175
- For x5=35 and f5=5: 35⋅5=175
Now, sum these values:
∑(xi⋅fi)=30+150+25p+175+175=530+25p
Step 4: Set up the mean formula
The formula for the mean is given by:
¯x=∑(xi⋅fi)∑fi
Substituting the known values:
20.6=530+25p50
Step 5: Cross-multiply to solve for p
Cross-multiplying gives:
20.6⋅50=530+25p
Calculating 20.6⋅50:
1030=530+25p
Step 6: Isolate p
Now, isolate p:
1030−530=25p
500=25p
p=50025=20
Conclusion
The value of p is 20.
---
We know that the mean ¯x is given as 20.6. We also have the values of xi (the data points) and fi (the frequencies):
- xi=(10,15,p,25,35)
- fi=(3,10,25,7,5)
We need to find the total frequency ∑fi:
∑fi=3+10+25+7+5=50
Next, we calculate ∑(xi⋅fi):
- For x1=10 and f1=3: 10⋅3=30
- For x2=15 and f2=10: 15⋅10=150
- For x3=p and f3=25: p⋅25=25p
- For x4=25 and f4=7: 25⋅7=175
- For x5=35 and f5=5: 35⋅5=175
∑(xi⋅fi)=30+150+25p+175+175=530+25p
The formula for the mean is given by:
¯x=∑(xi⋅fi)∑fi
Substituting the known values:
20.6=530+25p50
Cross-multiplying gives:
20.6⋅50=530+25p
Calculating 20.6⋅50:
1030=530+25p
Now, isolate p:
1030−530=25p
500=25p
p=50025=20
The value of p is 20.
Topper's Solved these Questions
Similar Questions
The mean of the following data is 20.6. Find the value of 10 15 p 25 35 3 10 25 7 5
View SolutionIf the mean of the following data is 18.75. Find the value of p . xi : 10 15 p 25 30 fi : 5 10 7 8 2
View SolutionThe median of the following data is 50. Find the values of p and q, if the sum of the all the frequencies is 90.
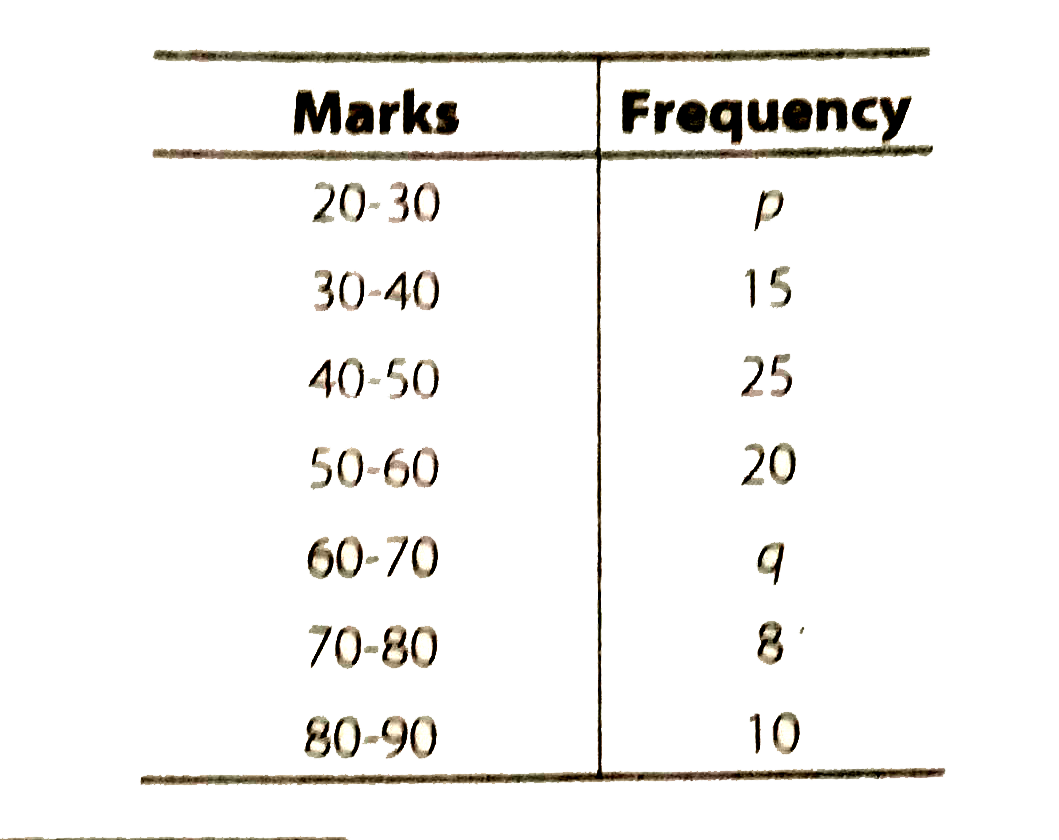 View Solution
View SolutionIf the mean of the following data is 20.2, then find the value of p.
 View Solution
View SolutionIf the mean of the following data is 26, then find the value of p:
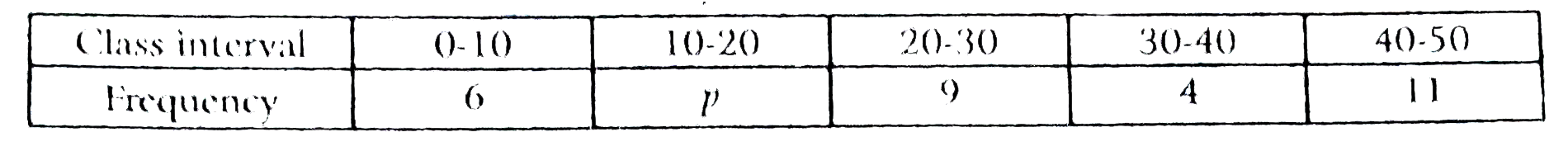 View Solution
View SolutionFind the mean of the following data :
 View Solution
View SolutionFind the mean of the following data :
 View Solution
View SolutionThe arithmetic mean of the following data is 14. Find the value of k xi : 5 10 15 20 25 fi : 7 k 8 4 5
View SolutionFind the mean of the following data:
View SolutionIf the mean of the following data is 5.6, find p :
 View Solution
View Solution

