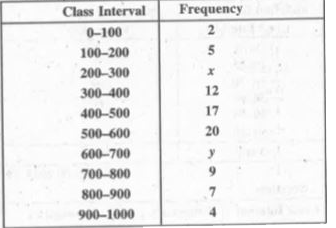
The median of the following data is 525. Find the values of x and y, if the total frequency is 100.
To solve the problem, we need to find the values of x and y given that the median of the data is 525 and the total frequency is 100.
1. Understanding the Median Formula:
The formula for the median in a continuous frequency distribution is given by:
Median=l+(n/2−cff)×h
where:
- l = lower limit of the median class
- n = total frequency
- cf = cumulative frequency of the class preceding the median class
- f = frequency of the median class
- h = width of the median class interval
2. Finding Cumulative Frequency:
We need to calculate the cumulative frequency for the given data. The cumulative frequency is the sum of the frequencies up to that class.
Let's assume the frequency distribution is as follows (for example):
- Class intervals: 400-500, 500-600, 600-700, etc.
- Frequencies: 2, 5, x, 12, 17, 20, y, 9, 7, 4
The cumulative frequencies will be:
- For 400-500: 2
- For 500-600: 2+5=7
- For 600-700: 7+x
- For 700-800: 7+x+12=19+x
- For 800-900: 19+x+17=36+x
- For 900-1000: 36+x+20=56+x
- For 1000-1100: 56+x+y
- For 1100-1200: 56+x+y+9
- For 1200-1300: 65+x+y+7
- For 1300-1400: 72+x+y+4=76+x+y
Since the total frequency is 100:
76+x+y=100
This gives us our first equation:
x+y=24(Equation 1)
3. Finding the Median Class:
Since the total frequency n=100, we find n/2=50. The median class is the class where the cumulative frequency is just greater than 50.
From our cumulative frequencies:
- The cumulative frequency before the median class is 36+x.
- The frequency of the median class (500-600) is 20.
Thus, the median class is 500-600.
4. Substituting Values into the Median Formula:
Now we substitute into the median formula:
525=500+(50−(36+x)20)×100
Simplifying this:
525=500+(14−x20)×100
525−500=(14−x20)×100
25=14−x20×100
25=5(14−x)
25=70−5x
5x=70−25
5x=45⇒x=9
5. Finding y:
Now substitute x=9 back into Equation 1:
9+y=24⇒y=24−9=15
Final Values:
Thus, the values of x and y are:
x=9,y=15
The formula for the median in a continuous frequency distribution is given by:
Median=l+(n/2−cff)×h
where:
- l = lower limit of the median class
- n = total frequency
- cf = cumulative frequency of the class preceding the median class
- f = frequency of the median class
- h = width of the median class interval
We need to calculate the cumulative frequency for the given data. The cumulative frequency is the sum of the frequencies up to that class.
- Class intervals: 400-500, 500-600, 600-700, etc.
- Frequencies: 2, 5, x, 12, 17, 20, y, 9, 7, 4
- For 400-500: 2
- For 500-600: 2+5=7
- For 600-700: 7+x
- For 700-800: 7+x+12=19+x
- For 800-900: 19+x+17=36+x
- For 900-1000: 36+x+20=56+x
- For 1000-1100: 56+x+y
- For 1100-1200: 56+x+y+9
- For 1200-1300: 65+x+y+7
- For 1300-1400: 72+x+y+4=76+x+y
76+x+y=100
This gives us our first equation:
x+y=24(Equation 1)
Since the total frequency n=100, we find n/2=50. The median class is the class where the cumulative frequency is just greater than 50.
- The cumulative frequency before the median class is 36+x.
- The frequency of the median class (500-600) is 20.
Now we substitute into the median formula:
525=500+(50−(36+x)20)×100
Simplifying this:
525=500+(14−x20)×100
525−500=(14−x20)×100
25=14−x20×100
25=5(14−x)
25=70−5x
5x=70−25
5x=45⇒x=9
Now substitute x=9 back into Equation 1:
9+y=24⇒y=24−9=15
Thus, the values of x and y are:
x=9,y=15
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.43videos
STATISTICS
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.26videos
STATISTICS
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.19videos
STATISTICS
- BOOK - NCERTCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - SOLVED EXAMPLES7videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.28videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
The median of the following data is 50. Find the values of p and q, if the sum of the all the frequencies is 90.
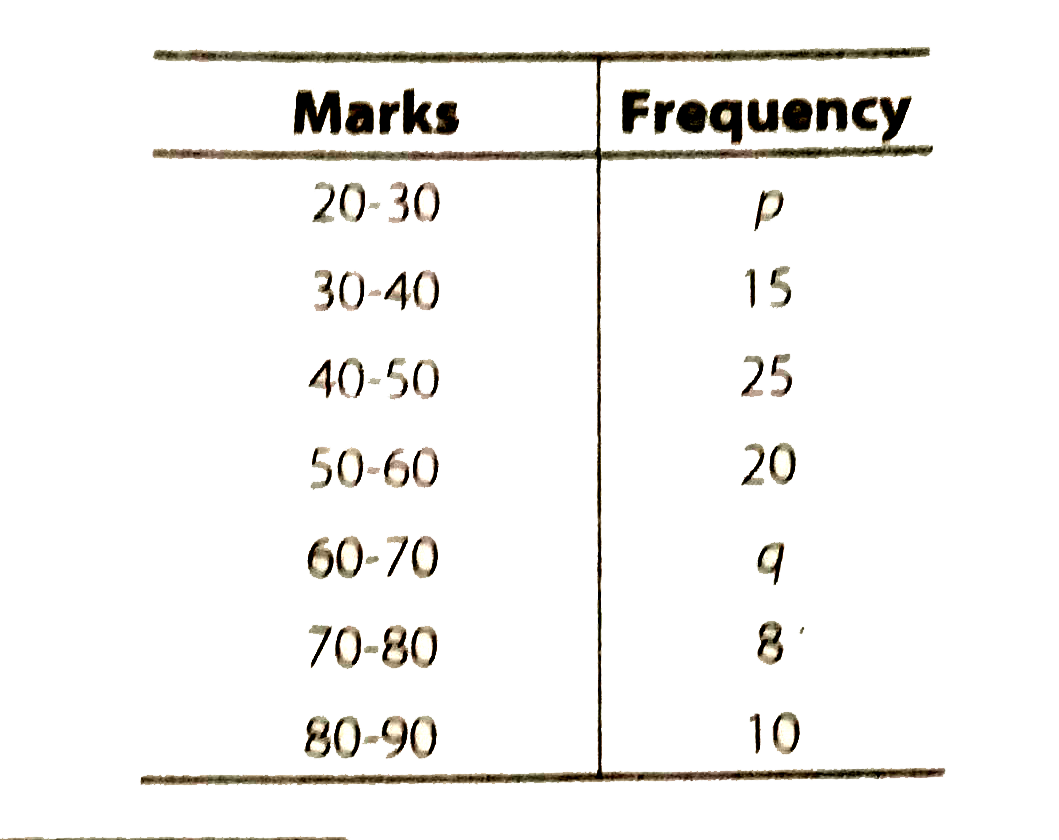 Ap=5 q=7Bp=2 q=6Cp=3 q=5Dp=5 q=8
Ap=5 q=7Bp=2 q=6Cp=3 q=5Dp=5 q=8
Find the median of the following data:
 View Solution
View SolutionFind the median of the following data:
 View Solution
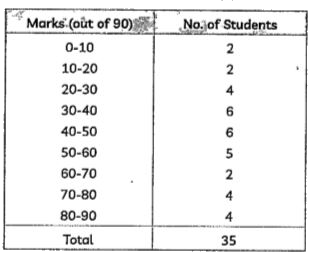
View SolutionFind the median of the following data.
View SolutionFind the median of the following data :
 View Solution
View SolutionFind the median of the following data :
 View Solution
View SolutionFind the median of the following data :
 View Solution
View SolutionFind the median of the following data.
 View Solution
View Solution