The medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
Let D is the mid-point of BC.
In ΔABC
D is the mid-point of BC
∴ area of ΔABD= area of ΔADC
(.: Median divides the triangle into two equal area)..(1)
In ΔGBC
D is the mid-point of BC
∴ area of ΔGBD= area of ΔGCD
(.: median divides the triangle into two equal area)..(2)
Subtract (2) from (1), we get
area of ΔABD− area of ΔGBD= area of ΔACD− area of ΔGCD
⇒ area of ΔABG= area of ΔACG....(3)
Similarly, we can prove that
area of ΔACG= area of ΔBCG
(∴ median divides the triangle into two equal area)...(4)
From (3) and (4), we get
area of ΔABG= area of ΔACG= area of ΔBCG
∴ area of ΔABG=13× area of ΔABC

Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
Three medians AD, BE and CF of ΔABC intersect at G. The area of ΔABC is 36 sq. cm. Then the area of ΔCGE is
A12 sq. cmB6 sq. cmC9 sq. cmD18 sq. cm - Question 2 - Select One
The three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
A10 sq.cmB15 sq.cmC20 sq.cmD30 sq.cm
D is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
 View Solution
View SolutionD is a point on the base BC of ΔABC.AD is produced upto E such that DE = AD. Prove that:
area of ΔBCE= area of ΔABCView SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
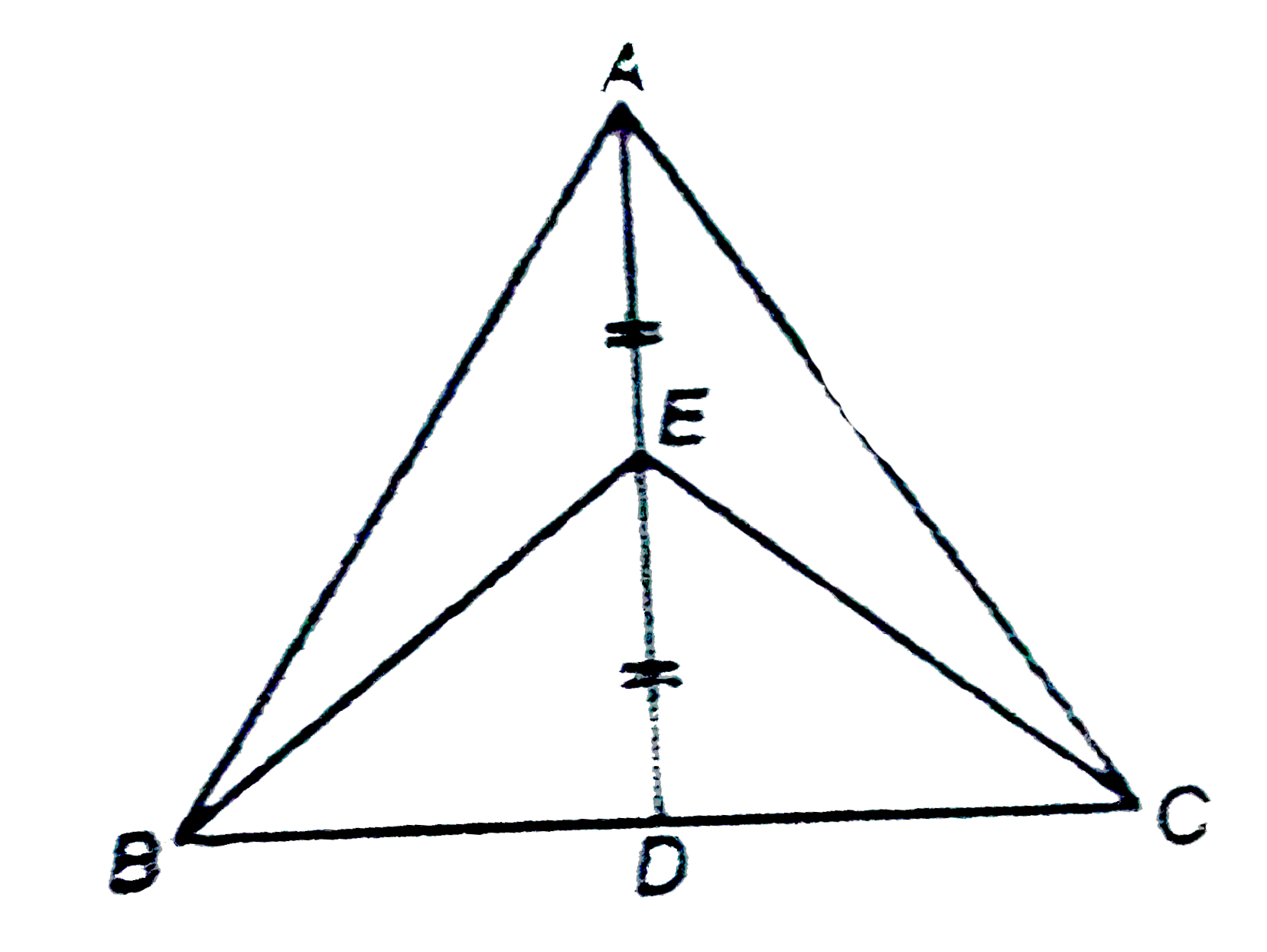 View Solution
View SolutionThe medians BE and CF of a triangle ABC intersect at G . Prove that area of GBC=areaofquadrilateralAGFE.
View SolutionIf the median AD and BE of a triangle ABC intersect at 0, prove that area of ΔAOB= area of quadrilateral CDOE.
View Solution


