The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
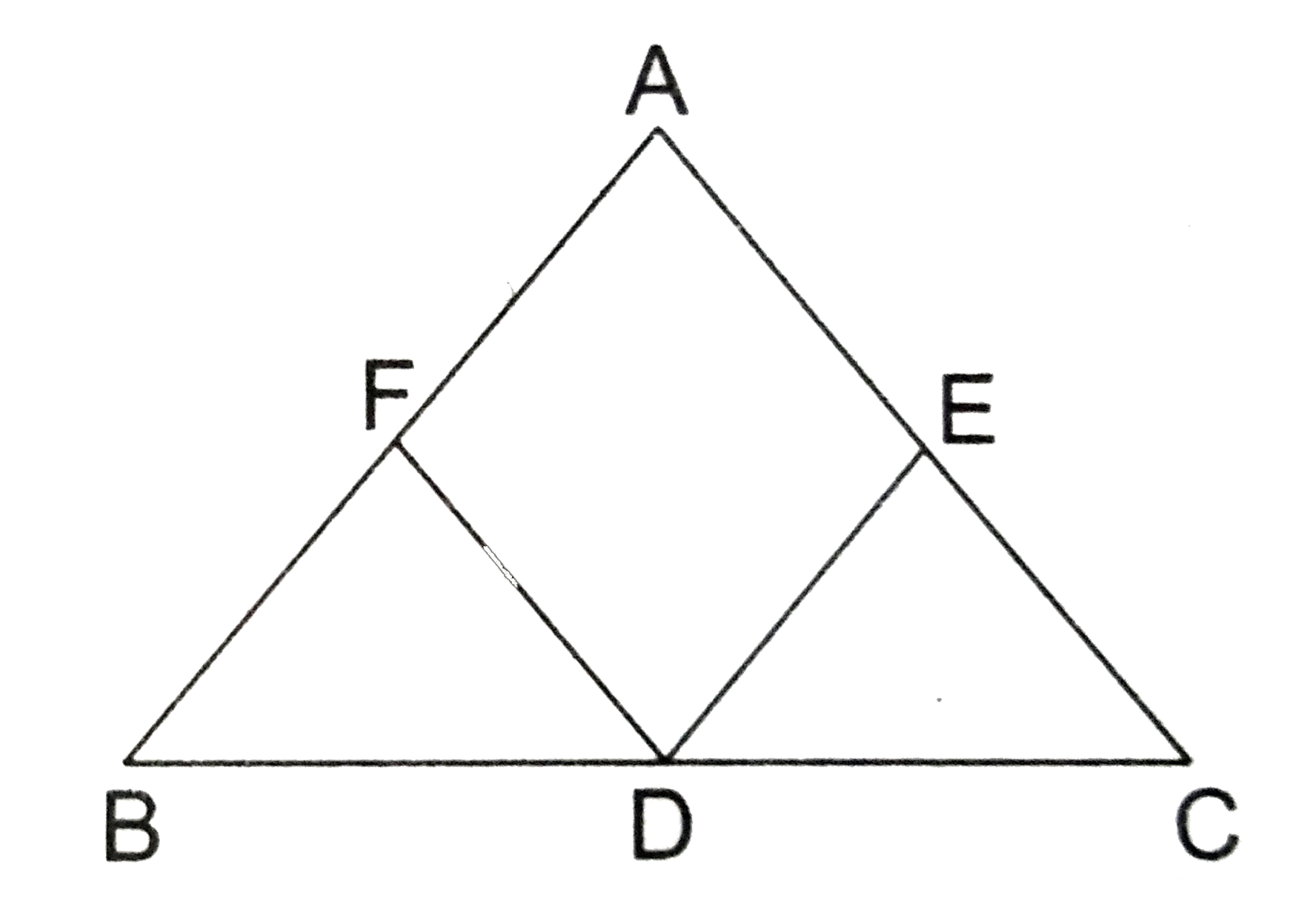
2(ar△ABC)
13(ar△ABC)
14(ar△ABC)
ar(△ABC)
The correct Answer is:A
Step by step video, text & image solution for The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
The mid points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(a)ar (ABC) (b) 12ar (ABC) 13ar (ABC) (d) 14 ar (ABC)
View SolutionThe midpoints of the sides of a triangle are (3, 4) , (4, 1) and (2, 0) . Find the vertices of the triangle .
View Solution
Knowledge Check
The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)Dar(△ABC)The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
A12ar(ABC)B13ar(ABC)C2ar(ABC)Dar(ABC)If the sides of a triangle are 4,5 and 6 cm, then area of the triangle is equal to :
A154cm2B154√7cm2C415√7cm2Dnone of these
The midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors.
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View SolutionIn an equilateral triangle another equilateral triangle is drawn inside joining the mid-points of the sides of given equilateral triangle and the process is continued up to 7 times. What is the ratio of area of fourth triangle to that of seventh triangle ?
View SolutionIf the sides of a triangle are 4,5 and 6 cm, then area of the triangle is equal to :
View Solution
