The minimum value of the fuction $f (x) = 2 | x - 2 | + 5 | x - 3 |$ for all $x \in R, i s$

A

3

B

2

C

5

D

7

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

We have ltbr gt $f (x) = 2 | x - 2 | + 5 | x - 3 |$
$= f (x) = {\begin{matrix} 2 (x - 2) + 5 (x - 3) = 7 x - 19 & x \geq 3 \\ 2 (x - 2) - 5 (x - 3) = - 3 x + 11 & 2 \leq x < 3 \\ - 2 (x - 2) - 5 (x - 3) = - 7 x = 19 & x < 2 \end{matrix}$

$\Rightarrow f (X) = {\begin{matrix} 7 & x > 3 \\ - 3 & 2 < x < 3 \\ - 7 & x < 2 \end{matrix}$
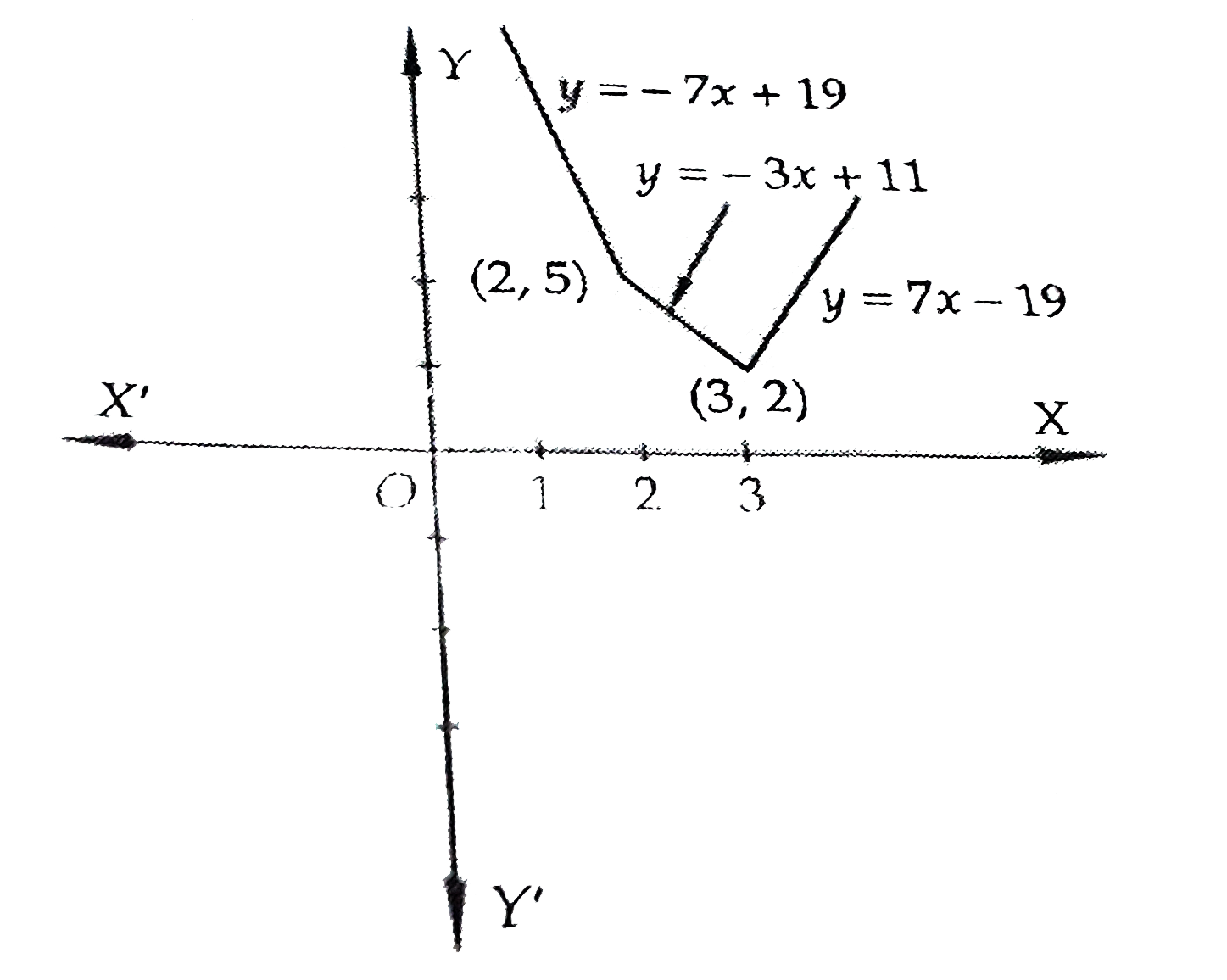
Clearly f(x) is increasing for all $x > 3$ .It decreases for $x > 2$ and also for $x \in (2, 3)$
$∴$ Minimum value of $f (x) = f (3) = 21 - 19 = 2$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The minimum value of the function
f(x) = 2|x - 1| + |x - 2| is
A0
B1
C2
D3
The minimum value of the function $f (x) = x^{3} - 3 x^{2} - 9 x + 5$ is :
A $- 9$
B10
C3
D16
The range of the fuction $f (x) = x^{2} + 2 x + 2$ is
A $(1, \infty)$
B $(2, \infty)$
C $(0, \infty)$
D $[1, \infty)$

OBJECTIVE RD SHARMA-MAXIMA AND MINIMA -Section I - Solved Mcqs

Home
Ask Doubt
Profile