If f(x) =∫x2x(t−1)dt,1≤x≤2 then the greatest value of ϕ (x) , is
A
2
B
4
C
8
D
none of these
Video Solution
Text Solution
The correct Answer is:B
We have ,
f(x)=x2∫x(t−1)dt
⇒f(x)=2x(x2−1)−(x−1)
⇒f(x)=2x3−3x+1
⇒f'(x)=(x−1)(2x2+2x−1)
⇒f(x)−2(x−1)(x+√3+12)(x−√3−12)
The signs of f(x) for different values for x are shown in Fig.26
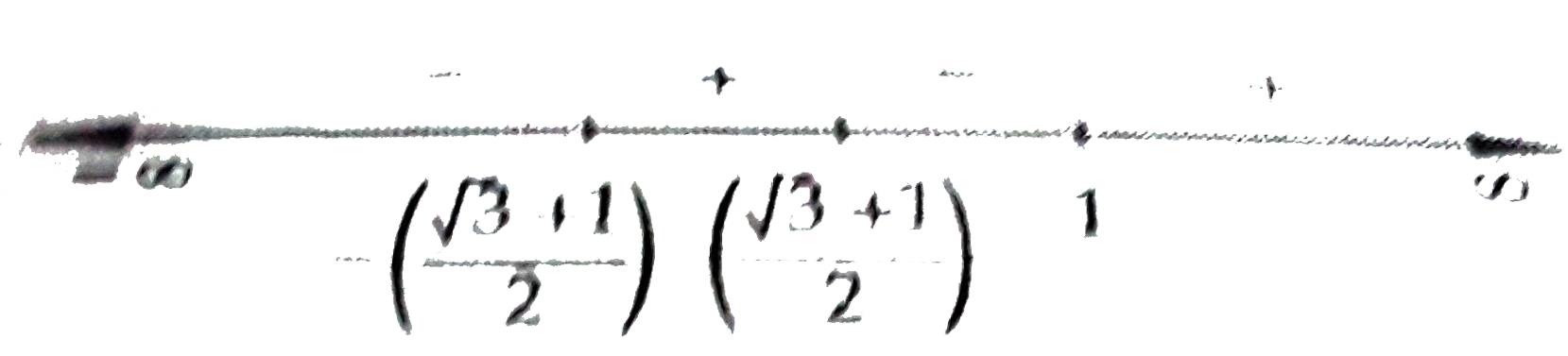
Clearly f'(x) >0 for all x∈[1,2] So, f(x) is increasing on [ 1.2]
Hence ,greatest value of f(x) is equal to
f(2)=4∫2[(t−1)22]42=4
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type7videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Exercise50videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test30videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test20videos
MATHEMATICAL REASONING
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
Similar Questions
Knowledge Check
- Question 1 - Select One
If∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) , is
A1/2B0C1D−1/2 - Question 2 - Select One
If ∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1), is
A1/2B0C1D−1/2 - Question 3 - Select One
If function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 then f is
Acontinous at x=0Bcontinous at x=1Ccontinous at x=-1Deverywhere continous
ϕ(x)=∫√x1/xsin(t2)dt, then find the value of ϕ′(1).
View SolutionIf f(x)={∫x0|1−t|dt;x>1,x−12;x≤1 then
View SolutionIf ∫x2(1+x)0f(t)dt=x, then the value of f(2) is.
View SolutionIf f(x) is continuous in [-2,2], where
f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩sinaxx−2,for−2≤x<02x+1,for0≤x≤12b√x2+3−1,for1<x≤2, then the value of (a+b) isView SolutionIf f(1x)+x2f(x)=0,x>0andI=∫x1/xf(t)dt,12≤x≤2x, then I is equal to
View Solution
