The number of complaints received on 8 different days of two different models of mobile phones sold by a shop are as follows:
Model A: 22 18 25 20 16 17 12 22
Model B: 16 14 22 12 14 20 10 12 What measure of central tendency should be used to determine which model is better? Find the measure of this central tendency and state which model has better performance?
The correct Answer is:Arithmetic mean ; model A, arithmetic mean = 19; model B. aritmetic mean = 15; Model B
To determine which model of mobile phone has better performance based on the number of complaints received, we will calculate the mean (average) number of complaints for both models. The model with the lower mean number of complaints will be considered better.
Step 1: Calculate the Mean for Model A
- List the complaints for Model A: 22, 18, 25, 20, 16, 17, 12, 22.
- Sum the complaints:
22+18+25+20+16+17+12+22=152
- Count the number of observations: There are 8 days.
- Calculate the mean:
Mean of Model A=Sum of complaintsNumber of observations=1528=19
Step 2: Calculate the Mean for Model B
- List the complaints for Model B: 16, 14, 22, 12, 14, 20, 10, 12.
- Sum the complaints:
16+14+22+12+14+20+10+12=130
- Count the number of observations: There are 8 days.
- Calculate the mean:
Mean of Model B=Sum of complaintsNumber of observations=1308=15
Step 3: Compare the Means
- Mean of Model A = 19
- Mean of Model B = 15
Conclusion:
Since Model B has a lower mean number of complaints (15) compared to Model A (19), Model B is considered to have better performance.
- List the complaints for Model A: 22, 18, 25, 20, 16, 17, 12, 22.
- Sum the complaints:
22+18+25+20+16+17+12+22=152
- Count the number of observations: There are 8 days.
- Calculate the mean:
Mean of Model A=Sum of complaintsNumber of observations=1528=19
- List the complaints for Model B: 16, 14, 22, 12, 14, 20, 10, 12.
- Sum the complaints:
16+14+22+12+14+20+10+12=130
- Count the number of observations: There are 8 days.
- Calculate the mean:
Mean of Model B=Sum of complaintsNumber of observations=1308=15
- Mean of Model A = 19
- Mean of Model B = 15
Since Model B has a lower mean number of complaints (15) compared to Model A (19), Model B is considered to have better performance.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DATA HANDLING AND MEASURES OF CENTRAL TENDENCYEXERCISE - EXERCIES 18.216videos
DATA HANDLING AND MEASURES OF CENTRAL TENDENCY
- BOOK - ICSECHAPTER - DATA HANDLING AND MEASURES OF CENTRAL TENDENCYEXERCISE - REVISION EXERCISE39videos
DATA HANDLING AND MEASURES OF CENTRAL TENDENCY
- BOOK - ICSECHAPTER - DATA HANDLING AND MEASURES OF CENTRAL TENDENCYEXERCISE - TRY THIS19videos
DATA HANDLING AND MEASURES OF CENTRAL TENDENCY
- BOOK - ICSECHAPTER - CONSTRUCTIONS EXERCISE - REVISION EXERCISE12videos
CONSTRUCTIONS
- BOOK - ICSECHAPTER - DATA HANDLING EXERCISE - EXERCISE 24D13videos
DATA HANDLING
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the mode in each of the following data collection.
12,13,12,15,16,16,13,12,14,18,12,12,14,15,19,12,14A10B12C9D8
The most stable measure of central tendency is
View SolutionEmpiricla relationship between the three measures of central tendency is
View SolutionWhich central tendency has been used to arrive at the following statements?
Mickey noticed that half of the chocolate brands in the store cost more than 22.View SolutionWhich of the following is not a measure of central tendency? (a) Mean (b) Median (c) Mode (d) Standard deviation
View SolutionThe salaries of 14 employes in a company are as follows.
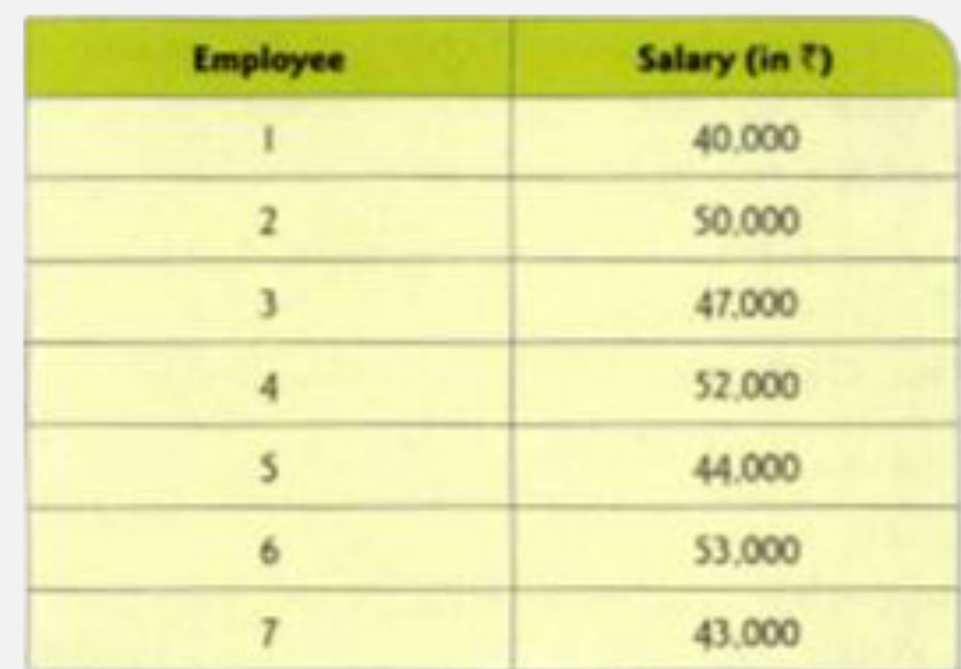

Which central tendency should be used to represent the salaries of the empolyes of the company?View SolutionWhich central tendency has been used to arrive at the following statements?
The weights of players in the football team vary by 12 kg.View SolutionFind the median of :
25, 18, 13, 20, 16, 9, 22, 8, 6, 15, 21, 11, 17View Solution

