The number of integral point inside the triangle made by the line 3x+4y−12=0 with the coordinate axes which are equidistant from at least two sides is/are :
( an integral point is a point both of whose coordinates are integers. )
1
2
3
4
The correct Answer is:A
Step by step video solution for The number of integral point inside the triangle made by the line 3x + 4y - 12 =0 with the coordinate axes which are equidistant from at least two sides is/are : ( an integral point is a point both of whose coordinates are integers. ) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-2 : One or More than One Answer is/are Correct12videos
STRAIGHT LINES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-3 : Comprehension Type Problems4videos
STRAIGHT LINES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems11videos
SOLUTION OF TRIANGLES
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems9videos
TRIGONOMETRIC EQUATIONS
Similar Questions
The incentre of the triangle formed by the line 3x+4y−12=0 with the coordinate axis is
View SolutionProve that all the vertices of an equilateral triangle can not be integral points (an integral point is a point both of whose coordinates are integers).
View SolutionFind the number of integral points which lie on or inside the circle x2+y2=4.
View SolutionThe number of integral points on the hyperbola x2−y2=(2000)2 is (an integral point is a point both of whose co-ordinates are integer) (A) 98 (B) 96 (C) 48 (D) 24
View SolutionThe number of integral points on the hyperbola x2−y2=(2000)2 is (an integral point is a point both of whose co-ordinates are integer) (A) 98 (B) 96 (C) 48 (D) 24
View SolutionPoint (0,β) lies on or inside the triangle fromed by the lines y=0,x+y=8 and 3x−4y+12=0. Then β can be :
View SolutionThe point at which the two coordinate axes meet is called the
View SolutionThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
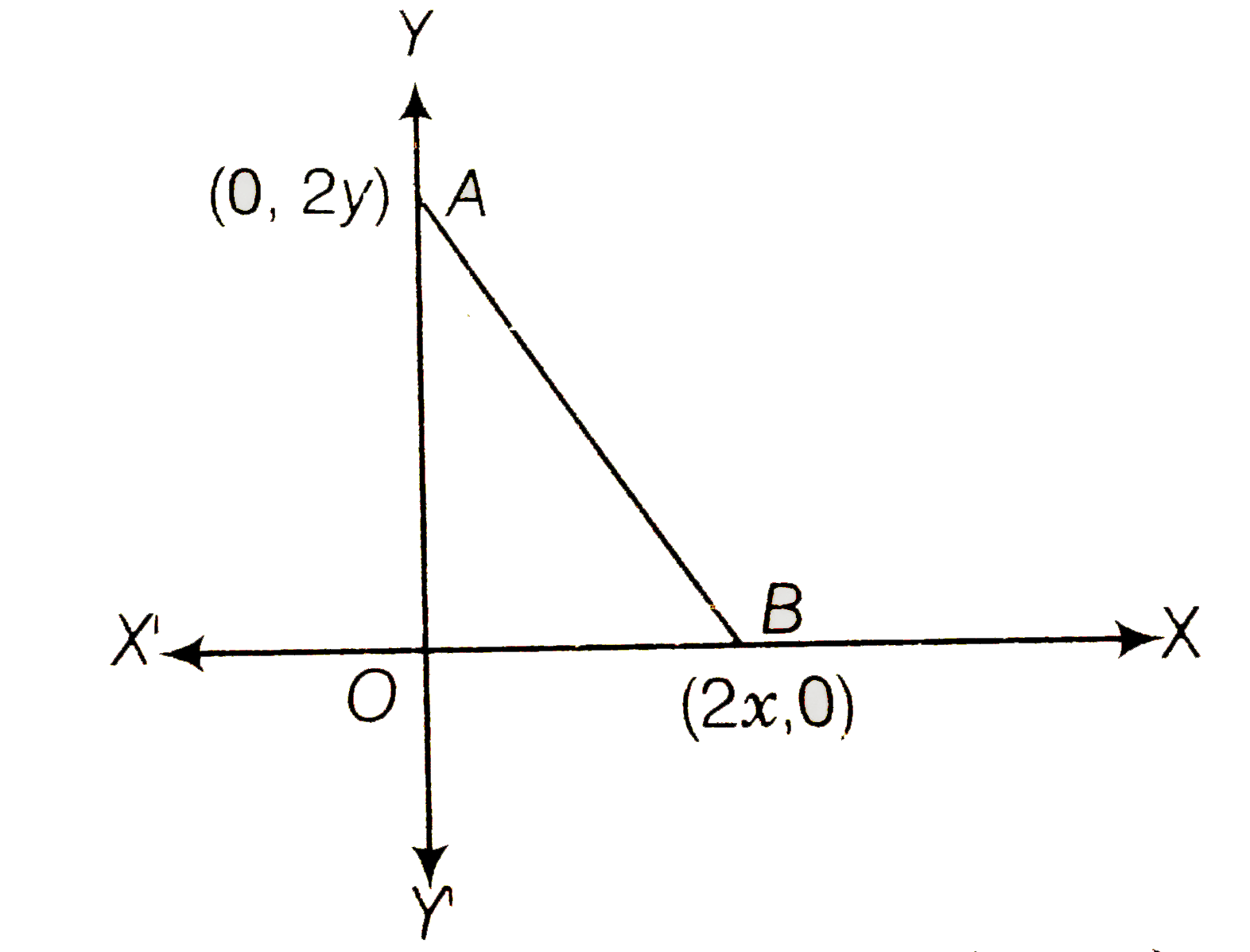 View Solution
View SolutionIf the 4 points made by intersection of lines 2x−y+1=0,x−2y+3=0 with the coordinate axes are concylic then centre of circle is
View SolutionWrite the coordinates of a point on X -axis which is equidistant from the points (−3, 4) and (2, 5) .
View Solution

