The number of ordered pairs (x,y) of real numbers that satisfy the simultaneous equations
x+y2=x2+y=12 is
A
0
B
1
C
2
D
4
Video Solution
Text Solution
The correct Answer is:D
x+y2=x2+y=12
curve(1)x+y2=12 curve(2)x2+y=12
y2=−(x−12) x2=−(y−12)
Intersection on x-axis (2,0) Intersection on x-axis =(±√12,0)
Intersection on y-zxis (0,±√12) Intersectionony−aξs=(0,12)
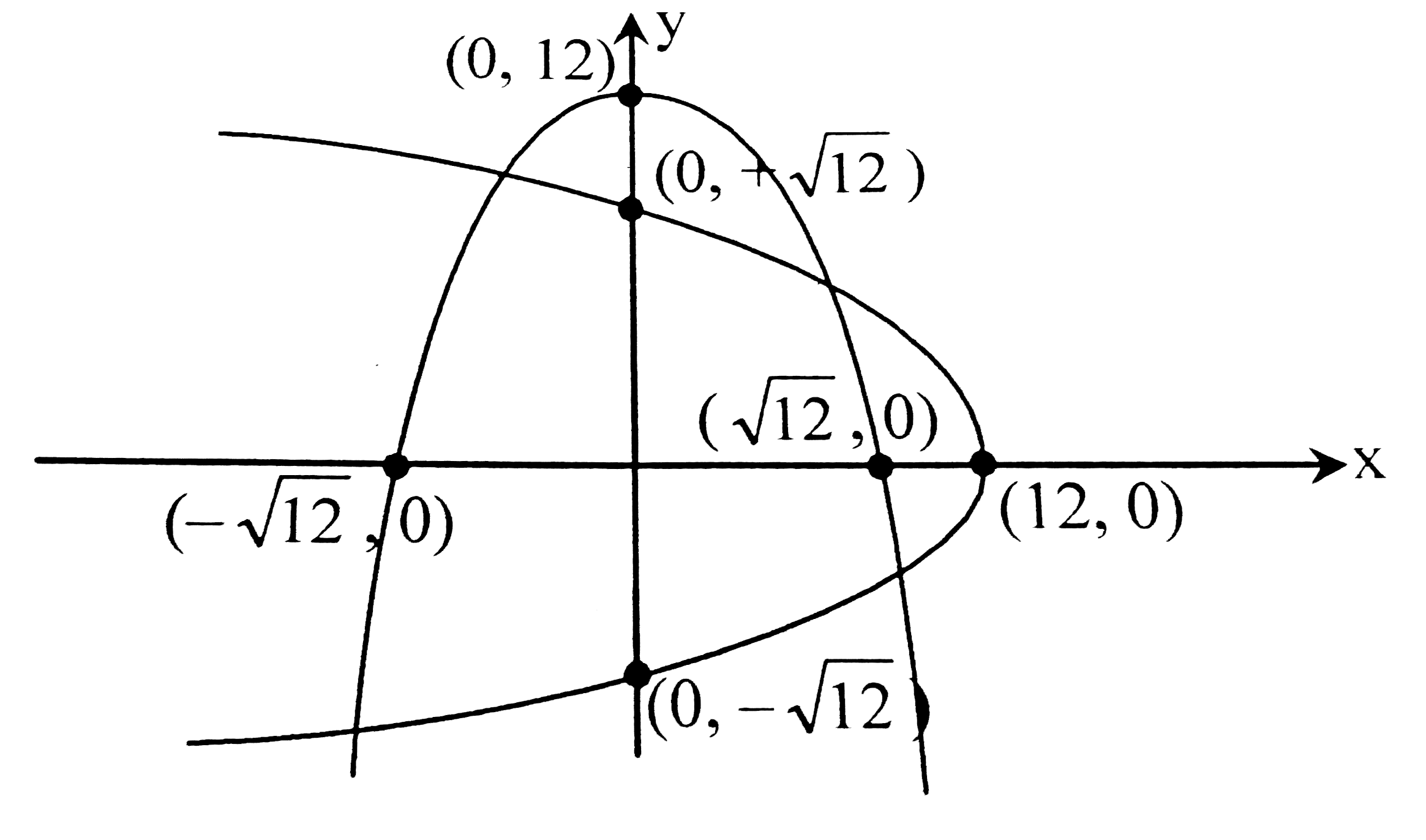
four intersection
|
Similar Questions
Knowledge Check
The number of ordered pair(s) (x,y) of real numbers satisfying the equation 1+x2+2xsin(cos−1y)=0, is :
A0B1C2D3The number of ordered pairs (x, y) of integers satisfying x3+y3=65 is
A0B2C4D6The number of all possible ordered pairs (x, y) x, y ∈ R satisfying the system of equations
x+y=2π3,cosx+cosy=32, isA0B1CinfiniteDnone of these
Find the number of ordered pair of real numbers (x, y) satisfying the equation:
5x(1+1x2+y2)=12&5y(1−1x2+y2)=4
View SolutionFind the number of ordered pairs (x, y) of integers which satisfies the following system of equations Xx+y=Y12yy+x=X3.
View SolutionNumber of pairs (x,y) real number that satisfy 2x2+y2+2xy−2y+2=0, is
View SolutionThe number of ordered pairs of positive integral (x,y), that satisfy the equation 1x+1y=12004
View SolutionThe number of all possible ordered pairs (x,y),x,y∈R satisfying the system of equations x+y=2π3,cosx+cosy=32 is
View Solution
