The number of polynomials having zeroes as-2 and 5 is
1
2
3
more than 3
The correct Answer is:D
To find the number of polynomials having zeros at -2 and 5, we can follow these steps:
Step 1: Identify the zeros
The zeros of the polynomial are given as:
- α = -2
- β = 5
Step 2: Calculate the sum and product of the zeros
The sum of the zeros (α + β) is:
Sum=−2+5=3
The product of the zeros (α * β) is:
Product=−2×5=−10
Step 3: Form the polynomial using the sum and product
The general form of a quadratic polynomial with zeros α and β is given by:
P(x)=x2−(Sum)x+(Product)
Substituting the values we calculated:
P(x)=x2−3x−10
Step 4: Consider the effect of multiplying by a non-zero constant
A polynomial can be multiplied by any non-zero constant, and it will still have the same zeros. For example, if we multiply the polynomial by a constant k (where k≠0):
P(x)=k(x2−3x−10)
This will still have the zeros at -2 and 5.
Step 5: Conclusion on the number of polynomials
Since we can choose any non-zero constant k, there are infinitely many polynomials that can be formed with the zeros -2 and 5.
Final Answer
Thus, the number of polynomials having zeros as -2 and 5 is infinite.
---
The zeros of the polynomial are given as:
- α = -2
- β = 5
The sum of the zeros (α + β) is:
Sum=−2+5=3
Product=−2×5=−10
The general form of a quadratic polynomial with zeros α and β is given by:
P(x)=x2−(Sum)x+(Product)
Substituting the values we calculated:
P(x)=x2−3x−10
A polynomial can be multiplied by any non-zero constant, and it will still have the same zeros. For example, if we multiply the polynomial by a constant k (where k≠0):
P(x)=k(x2−3x−10)
This will still have the zeros at -2 and 5.
Since we can choose any non-zero constant k, there are infinitely many polynomials that can be formed with the zeros -2 and 5.
Thus, the number of polynomials having zeros as -2 and 5 is infinite.
Topper's Solved these Questions
- POLYNOMIALS BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - NCERT EXEMPLAR (Exercise -2.2)
12 Videos
- POLYNOMIALS BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - NCERT EXEMPLAR (Exercise -2.3)
10 Videos
- POLYNOMIALS BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - NCERT CORNER (Exercise -2.4)
6 Videos
- PAIR OF LINEAR EQUTIONS IN TWO VARIABLESBOOK - OSWAL PUBLICATIONCHAPTER - PAIR OF LINEAR EQUTIONS IN TWO VARIABLESEXERCISE - Case-Based MCQs
15 Videos
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Self Assessment
66 Videos
Similar Questions
Knowledge Check
A quadratic polynomial with zeroes -2 and 3, is :
A3x2−2x+6B2x2+3x−6Cx2−2x+6Dx2−x−6A quadratic polynomial with zeroes -2 and 3, is:
A3x2−2x+6B2x2+3x−6Cx2−2x+6Dx2−x−6A quadratic polynomial whose zeroes are 3 and -5, is
Ax2+2x−15Bx2−2x+15Cx2−8x+15Dx2+8x−15
Write a quadratic polynomial whose zeros are -7 and 5.
View SolutionFind the quadratic polynomial whose zeros are - 3 and -5.
View SolutionFind the number of zeros of the polynomial represented in Fig.
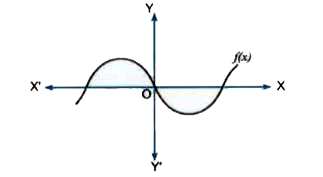
View SolutionFind a quadratic polynomial whose zeroes are −3and5.
View SolutionA quadratic polynomial whose zeros are 5and−3, is
View Solution
