The number of quadratic polynomials ax2+2bx+c which satisfy the following conditions is k
(i) a, b, c are distinct
(ii) a,b,c∈{1,2,3,4,….2001,2002}
(iii) x+1 divides ax+2bx+c Then k105 is equal to
The correct Answer is:20.02
To solve the problem, we need to find the number of distinct quadratic polynomials of the form ax2+2bx+c that satisfy the given conditions. Let's break down the solution step by step.
Step 1: Understand the conditions
We have the following conditions:
1. a,b,c are distinct.
2. a,b,c can take values from the set {1,2,…,2002}.
3. x+1 divides ax2+2bx+c.
Step 2: Use the divisibility condition
The condition that x+1 divides ax2+2bx+c means that substituting x=−1 into the polynomial should yield zero:
a(−1)2+2b(−1)+c=0⟹a−2b+c=0⟹c=2b−a.
Step 3: Determine the range for a and b
From the equation c=2b−a, we need to ensure that c is also in the range {1,2,…,2002}. This gives us the following inequalities:
1. 1≤c≤2002
2. 1≤2b−a≤2002
From the second inequality:
- 2b−a≥1⟹a≤2b−1
- 2b−a≤2002⟹a≥2b−2002
Step 4: Determine the valid range for a
Combining these inequalities, we have:
2b−2002≤a≤2b−1.
Since a must also be a distinct integer in the range {1,2,…,2002}, we must ensure:
- 2b−2002≥1⟹b≥1002
- 2b−1≤2002⟹b≤1001
However, since b must also be distinct from a and c, we can only take values of b from 1 to 1001.
Step 5: Count the valid pairs (a,b)
For each valid b from 1 to 1001:
- The value of a can take values from max(1,2b−2002) to min(2002,2b−1).
- The number of valid a values is given by:
Number of valid a=min(2002,2b−1)−max(1,2b−2002)+1.
Step 6: Calculate the total number of distinct polynomials
For each b, we compute the number of valid a values and then multiply by the number of choices for c (which is determined by c=2b−a).
Step 7: Calculate k
After calculating the total number of valid pairs (a,b), we find k and then compute k105.
Final Calculation
The final answer will be k105.
We have the following conditions:
1. a,b,c are distinct.
2. a,b,c can take values from the set {1,2,…,2002}.
3. x+1 divides ax2+2bx+c.
The condition that x+1 divides ax2+2bx+c means that substituting x=−1 into the polynomial should yield zero:
a(−1)2+2b(−1)+c=0⟹a−2b+c=0⟹c=2b−a.
From the equation c=2b−a, we need to ensure that c is also in the range {1,2,…,2002}. This gives us the following inequalities:
1. 1≤c≤2002
2. 1≤2b−a≤2002
- 2b−a≥1⟹a≤2b−1
- 2b−a≤2002⟹a≥2b−2002
Combining these inequalities, we have:
2b−2002≤a≤2b−1.
Since a must also be a distinct integer in the range {1,2,…,2002}, we must ensure:
- 2b−2002≥1⟹b≥1002
- 2b−1≤2002⟹b≤1001
For each valid b from 1 to 1001:
- The value of a can take values from max(1,2b−2002) to min(2002,2b−1).
- The number of valid a values is given by:
Number of valid a=min(2002,2b−1)−max(1,2b−2002)+1.
For each b, we compute the number of valid a values and then multiply by the number of choices for c (which is determined by c=2b−a).
After calculating the total number of valid pairs (a,b), we find k and then compute k105.
The final answer will be k105.
Topper's Solved these Questions
Similar Questions
Knowledge Check
if the number of quadratic polynomials ax2+2bx+c which satisfy the following conditions :
(i)a,b,c are distinct
(ii)a,b,c ∈ {1,2,3,….. , 2001,2002}
(iii)x+1 divides ax2+2bx+c is equal to 1000λ , then find the value of λ .A2002B2001C2003D2004If the zeroes of the quadratic polynomial ax2+bx+c,c≠0 are equal,then
Ac and a have opposite signsBc and b have opposite signsCc and a have the same signDc and b have the same signThe graph of a quadratic polynomial y=ax2+bx+c,a,b,c∈R is as shown.
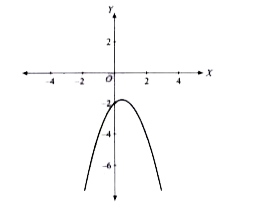
Which one of the is NOT correct ?Ab2−4ac<0Bca<0Cc is negativeDabscissa corresponding to the vertex is (−b2a)
If the zeroes of the quadratic polynomial ax2+bx+c, where c≠0, are equal, then
View SolutionThe graph of a quadratic polynomial ax2+bx+c=y(a,b,c,∈R,a≠0) then the incorrect statement is
View SolutionIf the quadratic polynomial is ax2+bx+c , then product of zeroes is ……… .
View SolutionIf one zero of a quadratic polynomial p(x)=ax2+bx+c is square of the other, then give the relation in a, b and c.
View SolutionIf x2+ax+1=0 is a factor of ax3+bx+c, then which of the following conditions are not valid
View Solution
