The objective function of a L.P.P is Solution in Tamil
constant
linear function to be optimised
relation between the variables
None of these
The correct Answer is:B
Step by step video, text & image solution for The objective function of a L.P.P is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - UNIT TEST6videos
LINEAR PROGRAMMING
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - LINEAR INEQUALITIESEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS38videos
LINEAR INEQUALITIES
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - MATHEMATICAL REASONINGEXERCISE - QUESTION FROM COMPETITIVE EXAMS23videos
MATHEMATICAL REASONING
Similar Questions
A company combines two items A and B from gift packs during a festival season. Each pack must weight atleast 5 kg and should contain atelast 2 kg of A and not more than 4 kg of B. The net contribution of the company is Rs. 10 per kg of A and Rs 12 per kg of B. the company wants to determine the optimum mix. By defining suitable variables, write
i. the objective function
ii. The constraintsView SolutionThe set of all x satisying the inequility 4x−13x+1≥1 is
View SolutionThe statement ~(p→q) is equivalent to
View SolutionL.P.P. is a process of finding
01:59View SolutionOptimization of the objective function is a process of
05:25View SolutionL.P.P. has constraints of
02:14View SolutionDefine the term ''objective function'' in an L.P.P.
02:56View SolutionDefine an objective function.
01:30View SolutionObjective function of a L.P.P. is
02:58View SolutionThe feasible region of an L.P.P is shown shaded in the figure. Let Z=3x−4 y be the objective function. The minimum of Z occurs at
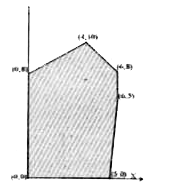 04:10View Solution
04:10View SolutionObjective function of a LPP is …………
03:47View SolutionIf the objective function for a L.P.P. is Z=5x+7y and the corner points of the bounded feasible region are (0, 0), (7, 0), (3, 4) and (0, 2), then the maximum value of Z occurs at
02:47View SolutionIf the objective function for an L.P.P. is Z=3x−4y and the corner points for the bounded feasible region are (0, 0), (5, 0), (6, 5), (6, 8), (4, 10) and (0, 8), then the maximum value of Z occurs at
03:53View SolutionIf the objective function for an L.P.P. is Z=3x+4y and the corner points for unbounded feasible region are (9, 0), (4, 3), (2, 5), and (0, 8), then the maximum value of Z occurs at
02:40View SolutionIf the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
01:19View Solution

