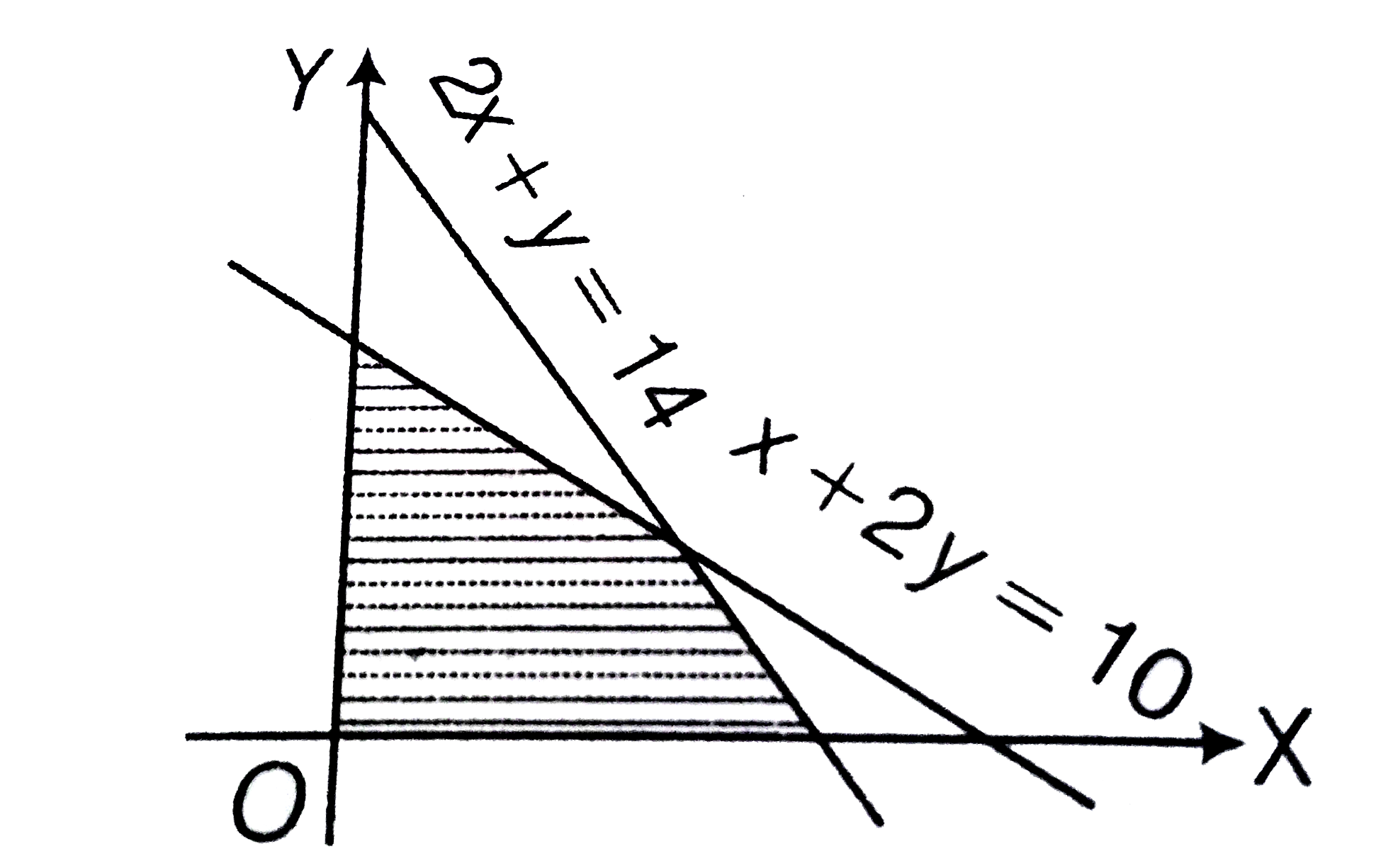
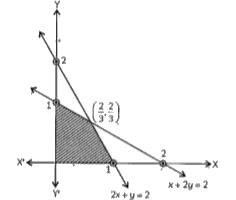
The optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
Video Solution
Text Solution
given by corner points of the feasible region
It is well known that the objective function's optimal value can be found at any of the corner points.
As a result, the optimal value of the objective function is found at the positions defined by the feasible region's corner points.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The optimal value of the objective function is attained at the points
Agiven by intersection of inequations with axes onlyBgiven by intersection of inequations with X-axis onlyCgiven by corner points of the feasible regionDNone of the aboveOne of the corner points of the feasible region of inequalities gives
AOptimal solution of LPPBObjective functionCConstraintsDLinear assumptionsConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IV
Maximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionIn the given figure, name:

lines whose point of intersection is C
View SolutionA, B C and D are the points of intersection with the coordinate axes of the lines ax+by=ab and bx+ay=ab, then
View SolutionAt the point of intersection of the two curves shown, the conc. of B is given by ……… for, A→nB:
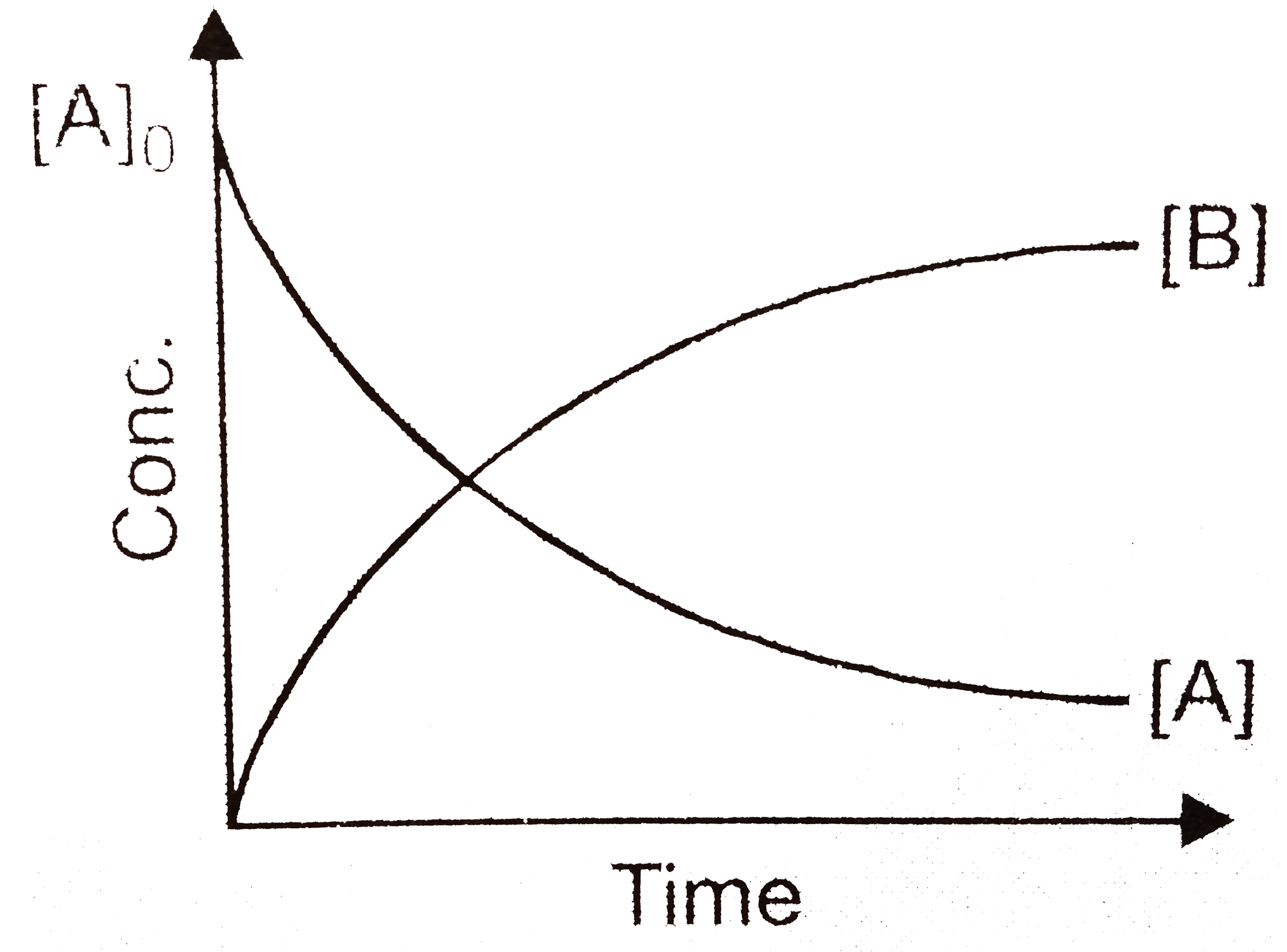
View Solution