The point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
Reflection of P(4,1) about the line y=x is Q(1,4). On translation of Q(1,4) through a distance of 2 units strong positive direction of x-axis, the point moves to R(1+2,4) or R(3,4).
On rotation about origin through an angle of π/4, the point R takes the position S such that OR=OS=5.
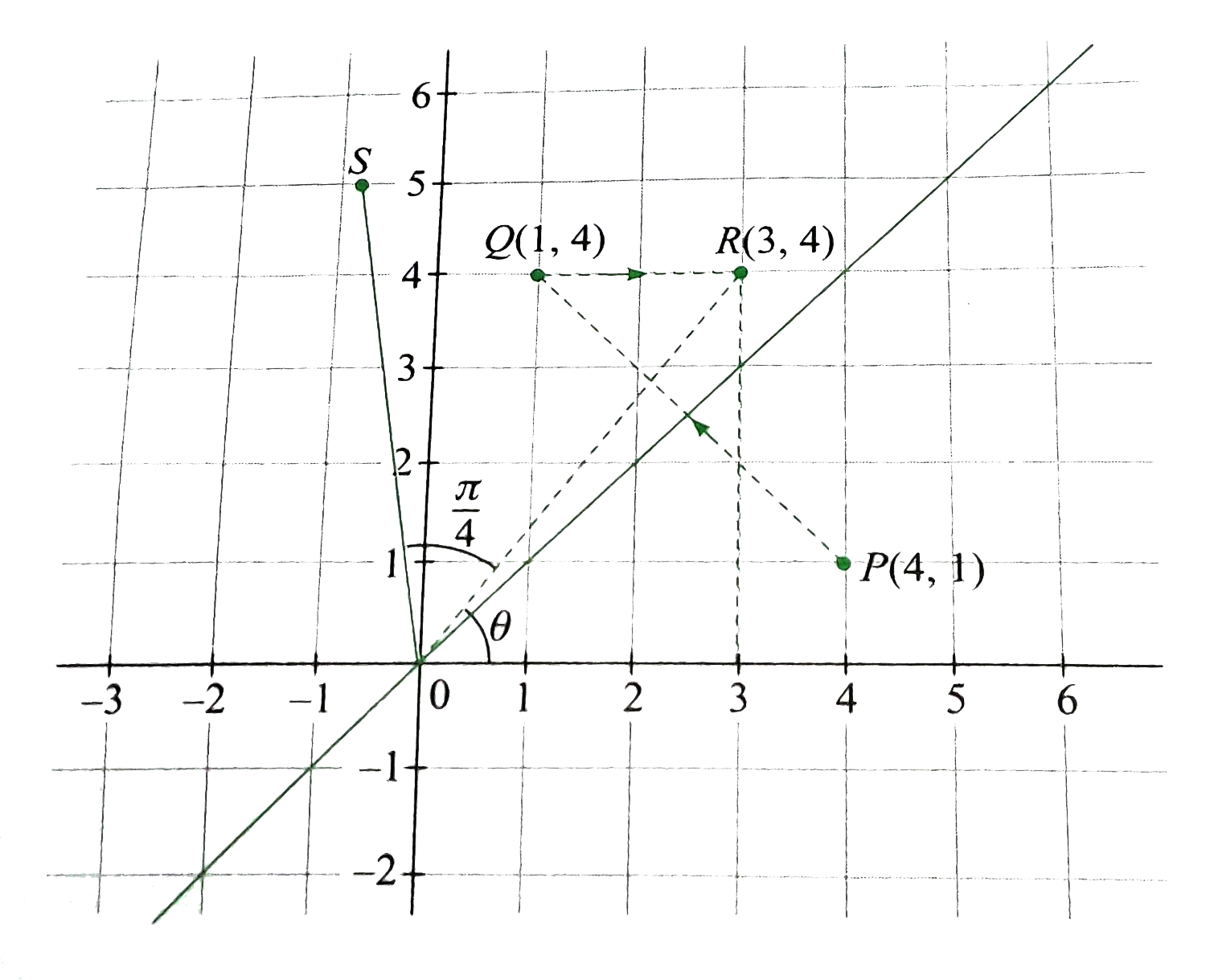
From the figure, cosθ=(35) and sinθ=(45) form trigonometric concepts, coordinates of point S are :
(5cos(π4+θ),=5(π4+θ))
Now , 5cos(π4+θ)=5(cosπ4cosθ−sinπ4sinθ)
=5(1√2.15−1√2.45)=−1√2
and 5sin(π4+θ)=5(sinπ4cosθ+sinθcosπ4)
(1√2.15+1√2.45)=7√2
Coordinates of S are (−1√2,7√2).
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.31videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.41videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main6videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
The point (4,1) undergoes the following three successive transformations ,
reflection about the line y=x−1
translation through a distance 1 unit along the positive direction
rotation thrpough an angle π4 about the origin in the anti - clockwise direction
Then the coordinates of the final point are ,
View SolutionThe point (4,1) undergoes the following two successive transformations
(i) Reflection about the line y=x
(ii) Translation through a distance 2 units along the positive X-axis.
Then the final coordinate of the point areView Solution
Knowledge Check
- Question 1 - Select One
The point (4,1) undergoes the following two successive transformations
(i) Reflection about the line y=x
(ii) Translation through a distance of 2 units along the positive x-axis.
The coordinates of the new point areA(4,3)B(3,4)C(1,4)D(73,72)
Find the position of point (4, 1) after it undergoes the transformations successively : Reflection about the line y=x−1
View SolutionA point (1, 1) undergoes reflection in the x-axis and then the coordinates axes are rotated through an angle of π4 in anticlockwise direction. The final position of the point in the new coordinate system is
View SolutionIf the axes are rotated through an angle of 30∘ in the anti clockwise direction, then coordinates of point (4,−2√3) with respect to new axes are
View SolutionFind the equation a line passing through (2,-3) and inclined at an angle of 150 with the positive direction of x-axis.
View SolutionA line passing through the point A(3,0) makes 300 angle with the positive direction of x- axis . If this line is rotated through an angle of 150 in clockwise direction, find its equation in new position.
View SolutionPoint P(2,3) goes through following transformations in successtion:
(i) reflection in line y=x
(ii) translation of 4 units to the right
(iii) translation of 5 units up
(iv) reflection in y-axis
Find the coordinates of final position of the point .View SolutionDetermine x so that the line passing through (3,4)and(x,5) makes an angle of 1350 with the positive direction of the x-axis.
View Solution

