The point which does not lie in the feasible region of 2x+3y<18 is :
(9, 0)
(0, 0)
(4, 1)
(1, 5)
The correct Answer is:A
To determine which point does not lie in the feasible region defined by the inequality 2x+3y<18, we will evaluate each given point against the inequality.
1. Identify the inequality: The inequality we need to check is 2x+3y<18.
2. Evaluate the first point (9, 0):
- Substitute x=9 and y=0 into the inequality:
2(9)+3(0)=18+0=18
- Since 18 is not less than 18, this point does not satisfy the inequality.
3. Evaluate the second point (0, 0):
- Substitute x=0 and y=0:
2(0)+3(0)=0+0=0
- Since 0<18, this point satisfies the inequality.
4. Evaluate the third point (4, 1):
- Substitute x=4 and y=1:
2(4)+3(1)=8+3=11
- Since 11<18, this point satisfies the inequality.
5. Evaluate the fourth point (1, 5):
- Substitute x=1 and y=5:
2(1)+3(5)=2+15=17
- Since 17<18, this point satisfies the inequality.
Conclusion
The point that does not lie in the feasible region of 2x+3y<18 is (9, 0).
- Substitute x=9 and y=0 into the inequality:
2(9)+3(0)=18+0=18
- Since 18 is not less than 18, this point does not satisfy the inequality.
- Substitute x=0 and y=0:
2(0)+3(0)=0+0=0
- Since 0<18, this point satisfies the inequality.
- Substitute x=4 and y=1:
2(4)+3(1)=8+3=11
- Since 11<18, this point satisfies the inequality.
- Substitute x=1 and y=5:
2(1)+3(5)=2+15=17
- Since 17<18, this point satisfies the inequality.
The point that does not lie in the feasible region of 2x+3y<18 is (9, 0).
Topper's Solved these Questions
- SAMPLE PAPER - 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 5EXERCISE - Section - B
20 Videos
- SAMPLE PAPER - 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 5EXERCISE - Section - C
10 Videos
- SAMPLE PAPER (SELF-ASSESSMENT) -10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF-ASSESSMENT) -10EXERCISE - SECTION - C
5 Videos
- SAMPLE PAPER 09BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 09EXERCISE - SECTIONS-C
8 Videos
Similar Questions
Knowledge Check
The point which does not lie in the half plane
2x+3y−12≤0 isA(1,2)B(2,1)C(2,3)D(-3,2)The point, which does not lie in the half-plane 3x+4y−15≤0 is:
A(1, 2)B(2, 1)C(2, 2)D(3, 2)The point, which does not lie in the half-plane 3x+4y−15≤0 is:
A(1,2)B(2,1)C(2,2)D(3,2)
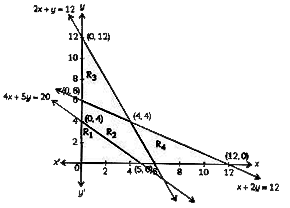
Which of the folowing should be the feasible region of the system of linear lnequalities x + 2y ≤12,2x+y≤12,4x+5y≥20 and x,y≥0 ?
View SolutionWhich of the following is a corner point of the feasible region of system of linear inequations 2x + 3y ≤6,x+4y≤4 and x, y ≥0 ?
View SolutionConsider the inequalities x1+x2≤3,2x1+5x2≥10x1,x2≥0 which of the following point does not lie in the feasible region ?
View SolutionWhich of the following is not a vertex of the feasible region bounded by the inequalities 2x+3y≤6,5x+3y≤15andx,y,≥0
View Solutionthe corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
View Solution
