The point which provides the solution of the linear programming problem, maximise Z = 45x + 55y. Subject to constraints Subject to constraints $x, y \geq 0, 6 x + 4 y \leq 120$ and $3 x + 10 y \leq 180$ is

A

(15, 10)

B

(10, 15)

C

(0,18)

D

(20,0)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given ,constriants are
$6 x + 4 y \leq 120$
$3 x + 10 y \leq 180$
$x, y \geq 10$
Objective function Z=45x+55y is to be maximised .

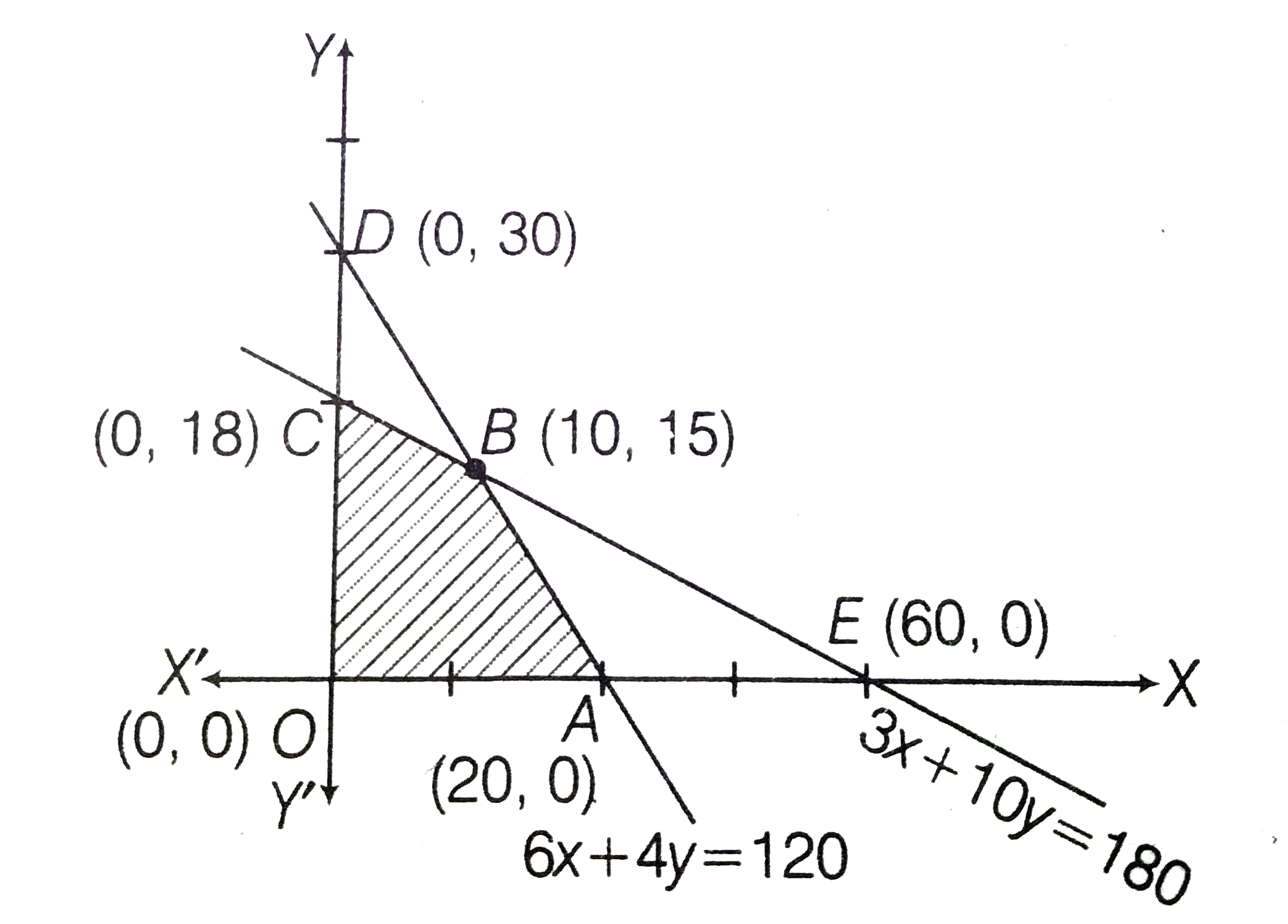
Here , OABCO is the requred feasible region whose corner points are O, A,B and C ,

Hence, the maximum value of Z is 1275 at B (10,15)

|

Updated on:21/07/2023

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Solve the linear programming problem. Maximise Z = x + 2y
Subject to constraints $x - y \leq 10, 2 x + 3 y \leq 20$ and $x \geq 0, y \geq 0$
AZ=10
BZ=30
CZ=40
DNone of these
Question 2 - Select One
The point which provides the solution of the solution to the linear programming problem . Maximum (2x+3y) subject to constraints .
$4 x + y \geq 4, x + 3 y \geq 6, x + y \geq 3, x \geq 0, y \geq 0$ is
A(3,2.5)
B(2.3.5 )
C(2,3.5)
D-1.35
Question 3 - Select One
Consider the linear programming problem Maximise Z = 4x + y.
Subject to constraints $x + y \leq 50, x + y \geq 100$ and $x, y \geq 0$ Then, maximum vlaue of Z is
A0
B50
C100
Ddoes not exist

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-Linear Programming -EXERCISE 2 (MISCELLANEOUS PROBLEMS )

Home
Ask Doubt
Profile