The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs (i) none (ii) not more than one (iii) more than one (iv) at least one will fuse after 150 days of use.
The correct Answer is:N/a
Let X represents the number of bulbs fused in 150 days in an experiment of 5 bulbs. It is the Bernaulli's experiment.
p=0.05 and q=1−p=1−0.05=0.95
X is a binomial distribution where n=5,p=0.05 and q=0.95.
∴P(X=r)=.5Cr.(0.05)r(0.95)5−r (i) Required Probability
=P(X=0)=.5C0p0q5=q5=(0.95)5
(ii) Required Probability
=P(X≤1)=P(0)+P(1)=.5_(0)p0q5+.5C1p1q4
=q5+5pq4=q4(q+5p)
=(0.95)4[0.95+5×(0.05)]
=(0.95)4(0.95+0.25)−(0.95)4×1.2
(iii) Required Probability
=P(X>1)=1p{P(0)+P(1)}
=1−(0.95)4×1.2
(iv) Required Probability
=P (at least one bulb will fuse)
=P(X≥1)=1P(0)
=1−(0.95)5
Topper's Solved these Questions
- PROBABIILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise
19 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Exercise 13.4
17 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs :
(i) none
(ii) none more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after an year of use is 0.1. Then the probability that out of 4 such bulbs, only one is working after an year
View Solution
Knowledge Check
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs none will fuse after 150 days of use?
A1−(1920)5B(1920)5C(34)5D90(14)5The probability that tulb produced by a factor will fuse after 150 days if used is 0.50. What is the probability that out of 5 such balbs none will fuse after 150 days of use ?
A1−(19/20)5B(19/20)5C(3/4)5D90(1/4)5
The probability that a bulb produced by a factory will fuse after 6 months of use is 0.05 . Find the probability that out of 5 such bulbs
(i) none will fuse after 6 months of use
(ii) at least one will fuse after 6 months of use
(iii) not more than one will fuse after 6 months of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 160 days of use is 0.06. Find the probability that out of 5 such bulbs at the most one bulb will fuse after 160 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days if used is 0.05. what is the probability that out of 5 such bulbs none will fuse after 150 days of use? 1−(1920)5 b. (1920)5 c. (34)5 d. 90(14)5
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. If a sample of such 5 bulbs are taken out, then match the probabilities in column I with their respective values in column II and choose the correct option from the codes given below.
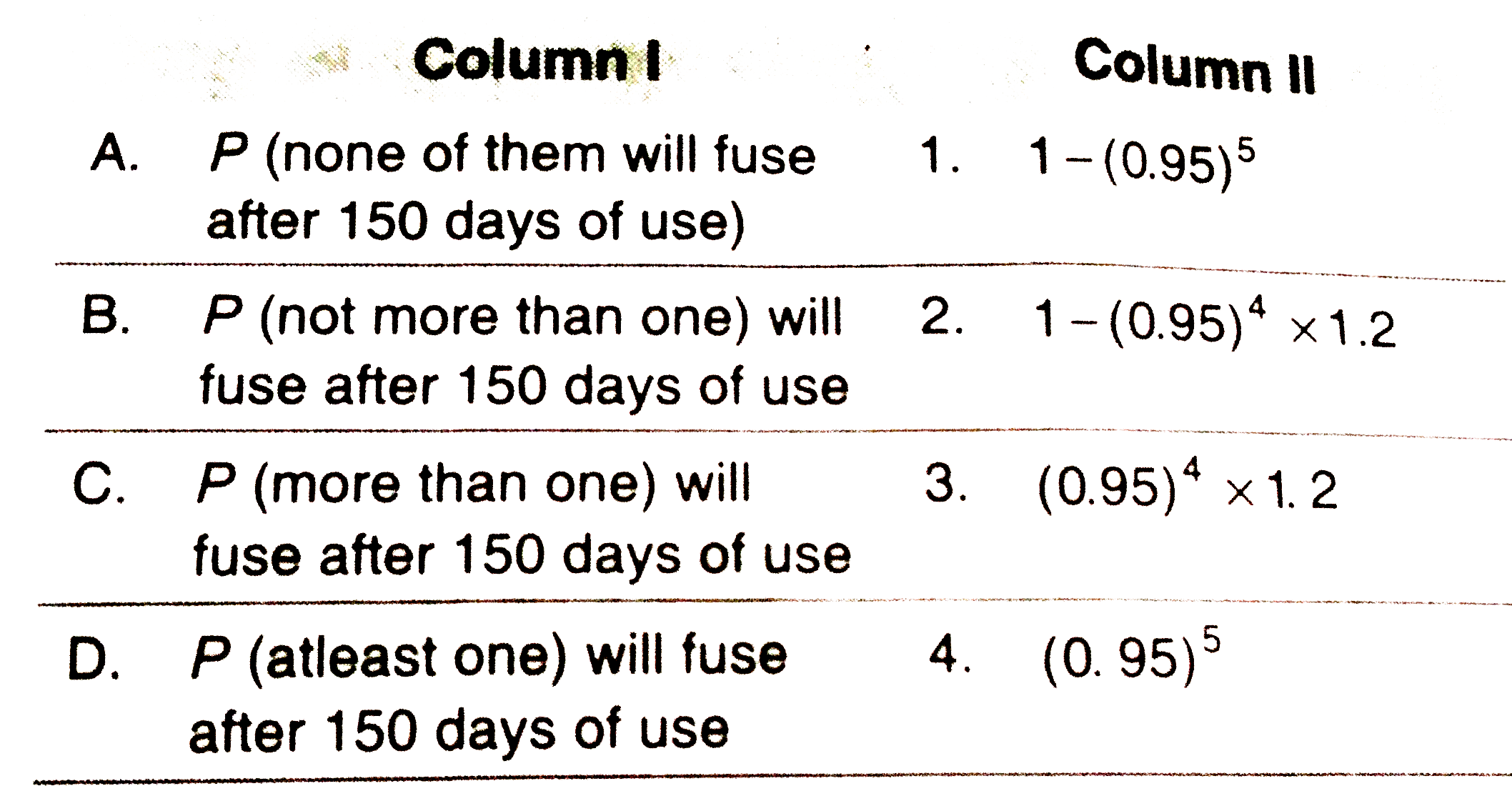
View SolutionThe probability that the life of a bulb is 100 days is 0.05. Find the probability that out of 6 bulbs (i) atleast 1 (ii) greater than 4 (iii) none will be having a life of 100 days
View SolutionThe probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5 ) that fuse after 200 days of use . Find the probability of
(i)X=0,(ii)X≤1,(iii)X>1,(iv)X≥1.
View Solution
