The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5 ) that fuse after 200 days of use . Find the probability of
(i)X=0,(ii)X≤1,(iii)X>1,(iv)X≥1.
The correct Answer is:i)(0.8)5ii)1.8×(0.8)4iii)1–(0.8)5iv)1−1.8×(0.8)4
To solve the problem, we will use the binomial probability formula, which is given by:
P(X=k)=(nk)pkqn−k
where:
- n is the total number of trials (in this case, 5 bulbs),
- k is the number of successes (bulbs that fuse),
- p is the probability of success (bulb fuses),
- q is the probability of failure (bulb does not fuse).
Given:
- p=0.2 (probability that a bulb fuses),
- q=1−p=0.8 (probability that a bulb does not fuse),
- n=5 (total number of bulbs).
Now, we will find the probabilities for each part of the question:
(i) Find P(X=0)
Using the binomial formula:
P(X=0)=(50)(0.2)0(0.8)5=1⋅1⋅(0.8)5
Calculating (0.8)5:
(0.8)5=0.32768
Thus,
P(X=0)=0.32768
(ii) Find P(X≤1)
This is the sum of the probabilities for X=0 and X=1:
P(X≤1)=P(X=0)+P(X=1)
We already calculated P(X=0). Now we calculate P(X=1):
P(X=1)=(51)(0.2)1(0.8)4=5⋅(0.2)⋅(0.8)4
Calculating (0.8)4:
(0.8)4=0.4096
Thus,
P(X=1)=5⋅0.2⋅0.4096=5⋅0.08192=0.4096
Now, adding both probabilities:
P(X≤1)=0.32768+0.4096=0.73728
(iii) Find P(X>1)
This can be calculated as:
P(X>1)=1−P(X≤1)
Thus,
P(X>1)=1−0.73728=0.26272
(iv) Find P(X≥1)
This can be calculated as:
P(X≥1)=1−P(X=0)
Thus,
P(X≥1)=1−0.32768=0.67232
Summary of Results:
- P(X=0)=0.32768
- P(X≤1)=0.73728
- P(X>1)=0.26272
- P(X≥1)=0.67232
- n is the total number of trials (in this case, 5 bulbs),
- k is the number of successes (bulbs that fuse),
- p is the probability of success (bulb fuses),
- q is the probability of failure (bulb does not fuse).
- p=0.2 (probability that a bulb fuses),
- q=1−p=0.8 (probability that a bulb does not fuse),
- n=5 (total number of bulbs).
- P(X=0)=0.32768
- P(X≤1)=0.73728
- P(X>1)=0.26272
- P(X≥1)=0.67232
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (ACTIVITIES)5videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - MATHEMATICAL LOGIC32videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (III. State whether each of the following is True or False.)9videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS9videos
PROBABILITY DISTRIBUTION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS8videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
The probability that a bulb produced by a factory will fuse after 160 days of use is 0.06. Find the probability that out of 5 such bulbs at the most one bulb will fuse after 160 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after an year of use is 0.1. Then the probability that out of 4 such bulbs, only one is working after an year
View Solution
Knowledge Check
- Question 1 - Select One
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs none will fuse after 150 days of use?
A1−(1920)5B(1920)5C(34)5D90(14)5 - Question 2 - Select One
The probability that tulb produced by a factor will fuse after 150 days if used is 0.50. What is the probability that out of 5 such balbs none will fuse after 150 days of use ?
A1−(19/20)5B(19/20)5C(3/4)5D90(1/4)5
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs :
(i) none
(ii) none more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.View SolutionThe probability that a bulb produced by a factory will fuse after 6 months of use is 0.05 . Find the probability that out of 5 such bulbs
(i) none will fuse after 6 months of use
(ii) at least one will fuse after 6 months of use
(iii) not more than one will fuse after 6 months of use.View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs(i) none(ii) not more than one(iii) more than one(iv) at least onewill fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days if used is 0.05. what is the probability that out of 5 such bulbs none will fuse after 150 days of use? 1−(1920)5 b. (1920)5 c. (34)5 d. 90(14)5
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. If a sample of such 5 bulbs are taken out, then match the probabilities in column I with their respective values in column II and choose the correct option from the codes given below.
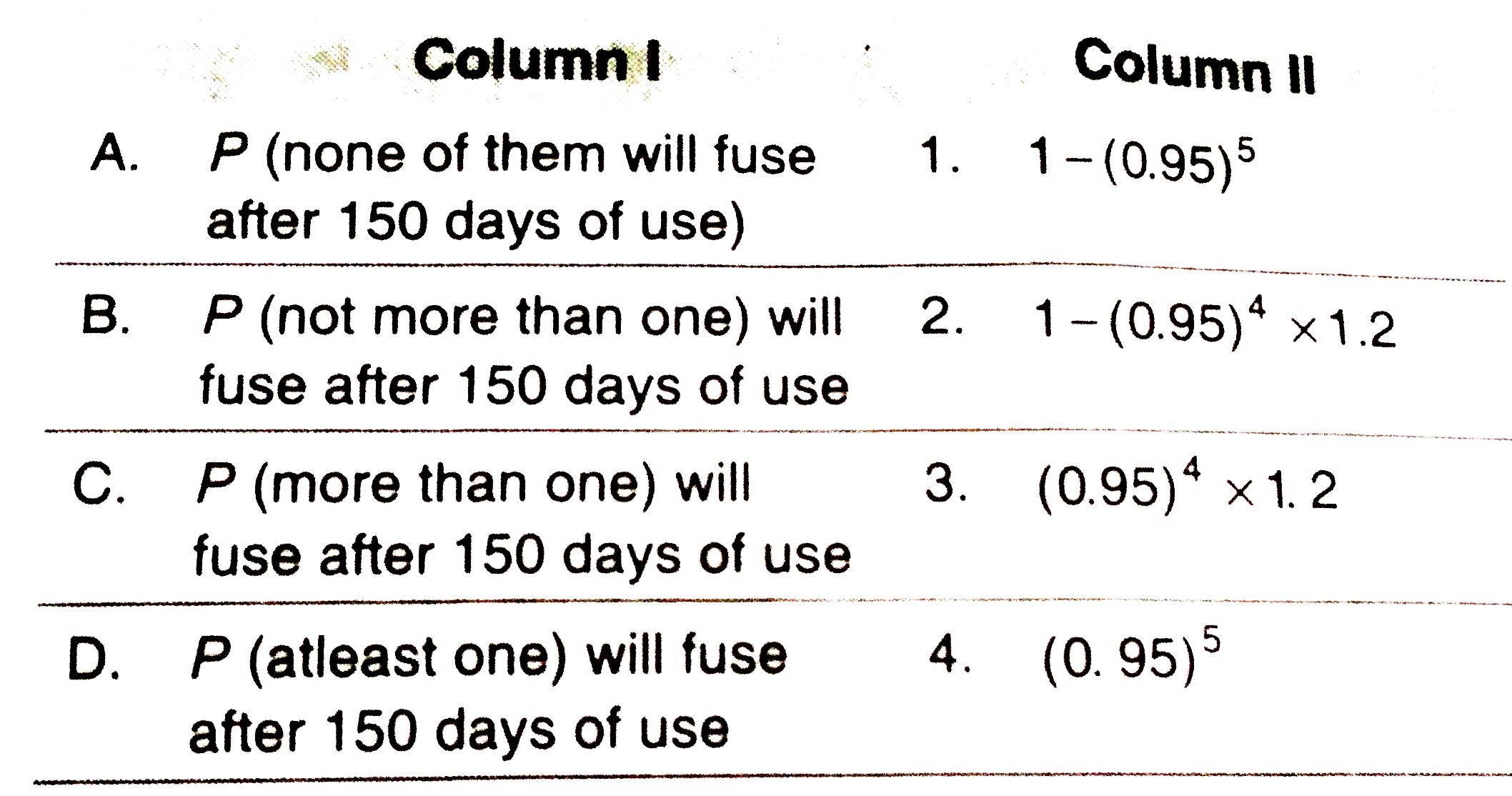 View Solution
View SolutionFind tha values of x2 for the given values of x. (i) x<2
(ii) x>−1
(iii) x≥2
(iv) x<−1View Solution

