The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
A
PQRS is a rectangle
B
PQRS is parallelogram
C
diagonals of PQRS are perpendicular
D
diagonals of PQRS are equal
Video Solution
Text Solution
The correct Answer is:C
Since, the quadrilateral ABCD formed by joining the mid-points of quadrilateral PQRS is a rectangle.
∴ AC=BD [since, diagonals of a rectangular are equal]
⇒ PQ=QR
Thus, quadrilateral PQRS is a rhombus.
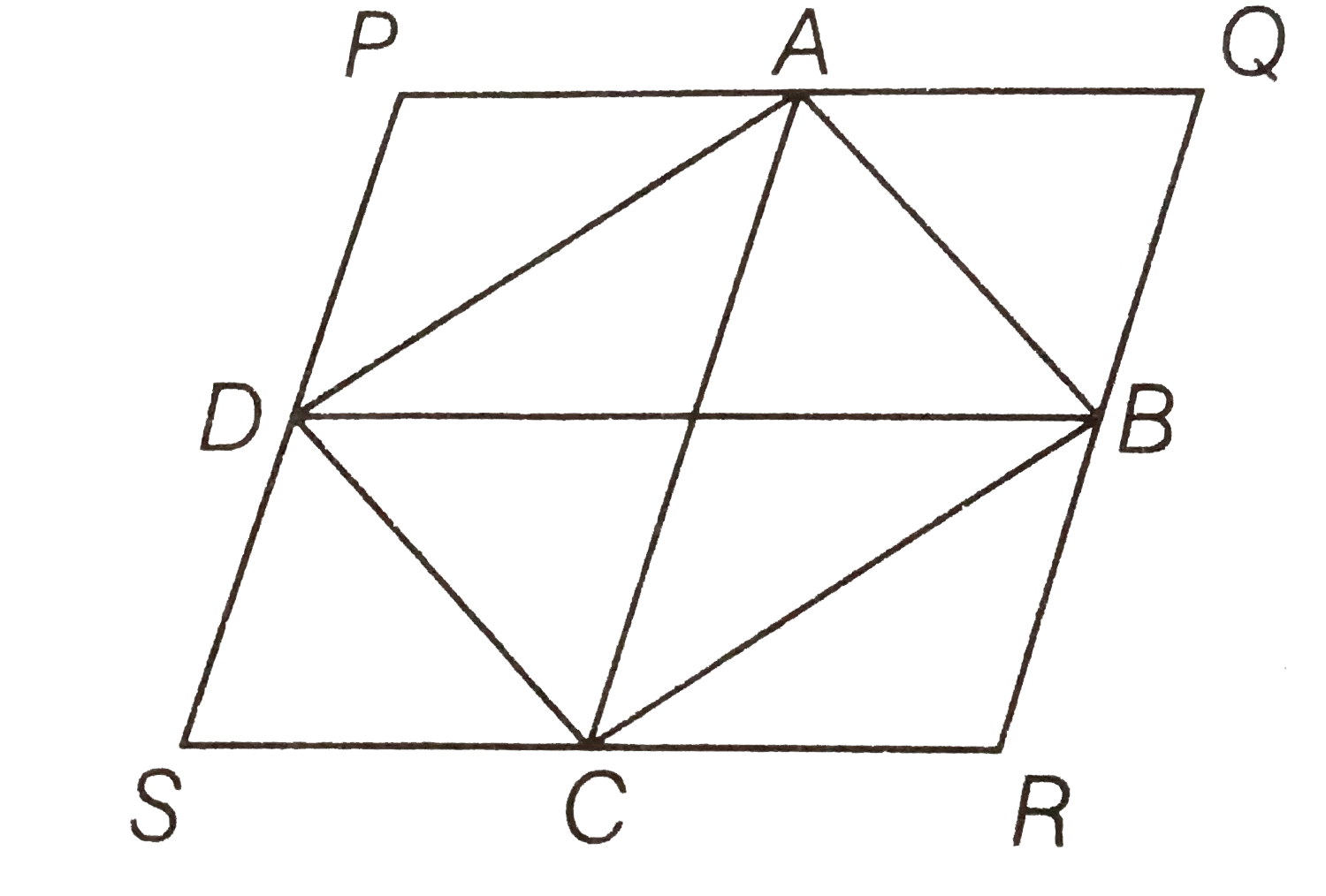
Hence, diagonals of PQRS i.e., PR and QS are perpendicular.
[since, diagonals of rhombus are perpendicular to each other]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rectangle, if
AABCD is a parallelogramBABCD is a rectangleCdiagonals of ABCD are equalDdiagonals of ABCD are perpendicular to each otherThe quadrilateral formed by joining the mid-points of the side for quadilateral PQRS, taken in order, is a rhombus, if
APQRS is a rhombusBPQRS is parallelogramCdiagonals of PQRS are perpendicularDdiagonals of PQRS are equalThe figure formed by joining the mid-points of the sides of a quadrilateral taken in order is
AparallelogramBrectangeCsquareDnone
Show that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionThe quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rhombus, if
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD taken in order is a square only, if
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if
View SolutionThe figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is
View Solution
