The random variable X has a probability distribution P(X) of the following form, where k is some arbitary real number:
P(X=x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩k,if x=02k,if x=13k,if x=20,otherwise
(i) Determine the value of k (ii) Find P(X<2),P(X≤2),P(X≥2)
The correct Answer is:k=16;P(X<2)=12;P(X≤2)=1;P(X≥2)=12
To solve the problem, we will break it down into two parts: determining the value of k and finding the required probabilities.
Part (i): Determine the value of k
1. Write the probability distribution:
The probability distribution is given as:
P(X=x)=⎧⎪
⎪⎨⎪
⎪⎩kif x=02kif x=13kif x=20otherwise
2. Use the property of probabilities:
The sum of all probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)=1
Substituting the values:
k+2k+3k=1
3. Combine like terms:
6k=1
4. Solve for k:
k=16
Part (ii): Find P(X<2), P(X≤2), and P(X≥2)
1. Calculate P(X<2):
P(X<2)=P(X=0)+P(X=1)=k+2k=3k
Substituting the value of k:
P(X<2)=3×16=36=12
2. Calculate P(X≤2):
P(X≤2)=P(X=0)+P(X=1)+P(X=2)=k+2k+3k=6k
Substituting the value of k:
P(X≤2)=6×16=1
3. Calculate P(X≥2):
P(X≥2)=P(X=2)+P(X>2)=3k+0=3k
Substituting the value of k:
P(X≥2)=3×16=36=12
Final Answers:
- k=16
- P(X<2)=12
- P(X≤2)=1
- P(X≥2)=12
The probability distribution is given as:
P(X=x)=⎧⎪
⎪⎨⎪
⎪⎩kif x=02kif x=13kif x=20otherwise
The sum of all probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)=1
Substituting the values:
k+2k+3k=1
6k=1
k=16
P(X<2)=P(X=0)+P(X=1)=k+2k=3k
Substituting the value of k:
P(X<2)=3×16=36=12
P(X≤2)=P(X=0)+P(X=1)+P(X=2)=k+2k+3k=6k
Substituting the value of k:
P(X≤2)=6×16=1
P(X≥2)=P(X=2)+P(X>2)=3k+0=3k
Substituting the value of k:
P(X≥2)=3×16=36=12
- k=16
- P(X<2)=12
- P(X≤2)=1
- P(X≥2)=12
Topper's Solved these Questions
- MODEL TEST PAPER-9BOOK - ICSECHAPTER - MODEL TEST PAPER-9EXERCISE - SECTION - B
10 Videos
- MODEL TEST PAPER-9BOOK - ICSECHAPTER - MODEL TEST PAPER-9EXERCISE - SECTION - C
10 Videos
- MODEL TEST PAPER-6BOOK - ICSECHAPTER - MODEL TEST PAPER-6EXERCISE - Section -C
10 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - MULTIPLE CHOICE QUESTIONS
82 Videos
Similar Questions
The random variable X has a probability distribution P(X) of the following form, where k is some number : P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise) (a) Determine k. (b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionA random variable X has the following distribution .

The value of k and P(X<4) are equal to
View SolutionIf a random variable X has a Poisson distribution such that P(X=1)=P(X=2) then
I: its mean is 2 II: its variance is 1
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X take the values of x has the following form, where k is some unknown constant. P(X=x)={(0.1ifx=0),(kx,ifx=1or2),(k(5−x),ifx=3or4),(0,otherwise)
Find:
(i) k
(ii) the probability that you study exactly two hours,
(iii) the probability that you study at most two hours.
View SolutionIn a Poisson distribution if P(X=0)=P(X=1)=k, the value of k is
View SolutionA random variable X has the following probability distribution:
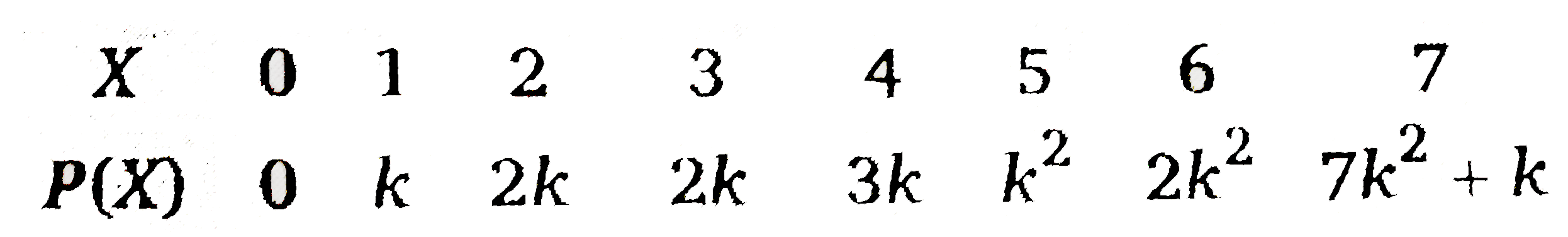
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionThe probability distribution for a random variable X is as follows:
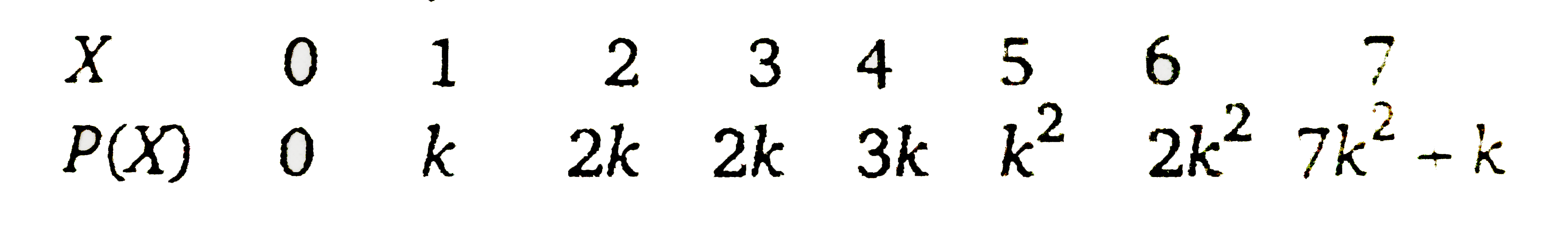
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
