If X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
The correct Answer is:14
To find the value of the constant C in the probability distribution P(X=k)=(k+1)C2k for k=0,1,2,…, we need to ensure that the total probability sums to 1. This is a fundamental property of probability distributions.
1. Set Up the Equation for Total Probability:
∞∑k=0P(X=k)=1
Substituting the expression for P(X=k):
∞∑k=0(k+1)C2k=1
2. Factor Out the Constant C:
C∞∑k=0(k+1)2k=1
3. Evaluate the Series ∞∑k=0(k+1)2k:
We can split this series into two parts:
∞∑k=0(k+1)2k=∞∑k=0k2k+∞∑k=012k
The second part is a geometric series:
∞∑k=012k=11−12=2
4. Evaluate ∞∑k=0k2k:
This can be derived using the formula for the sum of a series:
∞∑k=0kxk=x(1−x)2for |x|<1
Setting x=12:
∞∑k=0k(12)k=12(1−12)2=12(12)2=2
5. Combine the Results:
Therefore,
∞∑k=0(k+1)2k=2+2=4
6. Substitute Back into the Equation:
Now we have:
C⋅4=1
7. Solve for C:
C=14
Final Answer:
The value of the constant C is 14.
∞∑k=0P(X=k)=1
Substituting the expression for P(X=k):
∞∑k=0(k+1)C2k=1
C∞∑k=0(k+1)2k=1
We can split this series into two parts:
∞∑k=0(k+1)2k=∞∑k=0k2k+∞∑k=012k
The second part is a geometric series:
∞∑k=012k=11−12=2
This can be derived using the formula for the sum of a series:
∞∑k=0kxk=x(1−x)2for |x|<1
Setting x=12:
∞∑k=0k(12)k=12(1−12)2=12(12)2=2
Therefore,
∞∑k=0(k+1)2k=2+2=4
Now we have:
C⋅4=1
C=14
The value of the constant C is 14.
Similar Questions
If X is a random variable with probability distribution as given below: X=xi: 0 1 2 3 P(X=xi):k 3k 3k k The value of k and its variance are (A) 18,2227 (B) 18,2327 (C) 18,2427 (D) 18,34
View SolutionCheck the following distributions of probability of random variable X is the probability distributions?
X: 0 1 2
P(X):0.6 0.4 0.2
View SolutionLet X be a discrete random variable whose probability distribution is defined as follows: P(X=x)={k(x+1)forx=1,2,3,42kxforx=5,6,70otherwise , where k is a constant. Find (i) k (ii) E(X) (iii) standard deviation of X.
View SolutionThe random variable X has a probability distribution P(X) of the following form, where k is some number : P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise) (a) Determine k. (b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionA discrete random variable X has the probability distribution as given below
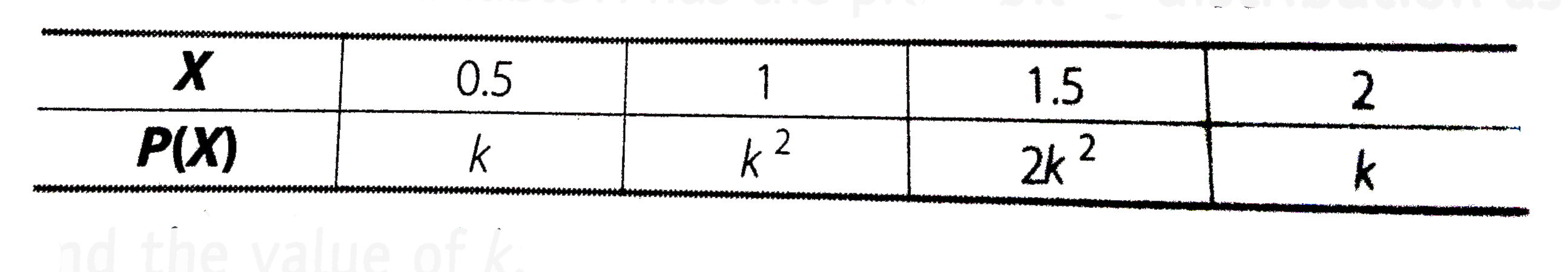
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution as given below
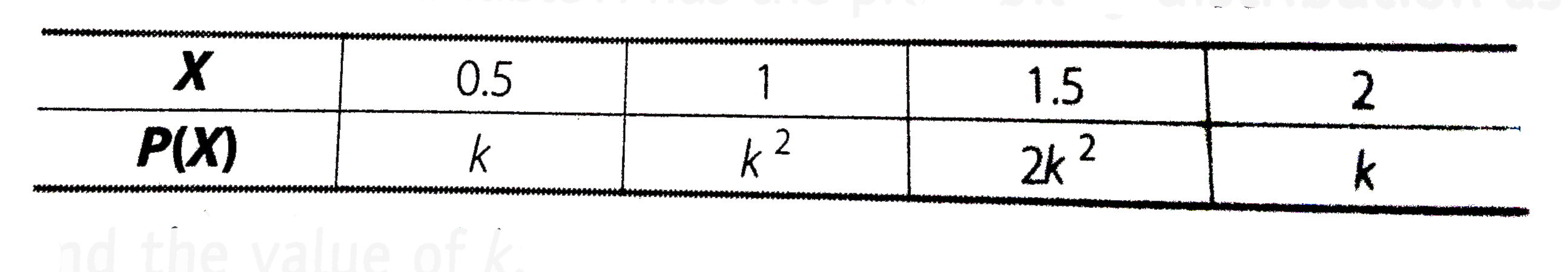
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionProve that the following distributions of probability of random variable X are the probability distributions? X: 0 1 2 3 4 P(X):0.1 0.5 0.2 0.1 0.1
View SolutionWhich of the following distributions of probability of random variable X are the probability distributions?
X: 0 1 2 3
P(X):0.3 0.2 0.4 0.1
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View Solution
