The random variable X has a probability distribution P(X) of the following form, where k is some arbitary real number:
P(X=x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩k,if x=02k,if x=13k,if x=20,otherwise
(i) Determine the value of k (ii) Find P(X<2),P(X≤2),P(X≥2)
The correct Answer is:N/a
The probability distribution of X is
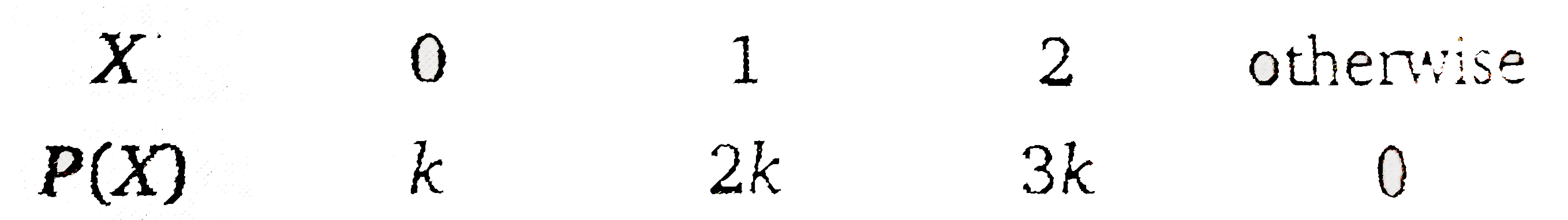
(a) Since ∑P(X)=1,
Therefore P(0)+P(1)+P(2)+P (otherwise) =1
⇒k+2k+3k+0=1⇒6k=1⇒k=16
(b) P(X<2)=P(0)+P(1)−k+2k=3k=3×16=12
P(X≤2)=P(0)+P(1)+P(2)=k+2k+3k=6k
=6×12=1
and P(X≥2)=P(2)+P (otherwise)
=3k+0=3×16=12
Topper's Solved these Questions
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Exercise 13.5
15 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise
19 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Exercise 13.3
14 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
The random variable X has a probability distribution P(X) of the following form, where k is some number : P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise) (a) Determine k. (b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionA random variable X has the following distribution .

The value of k and P(X<4) are equal to
View SolutionIf a random variable X has a Poisson distribution such that P(X=1)=P(X=2) then
I: its mean is 2 II: its variance is 1
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X take the values of x has the following form, where k is some unknown constant. P(X=x)={(0.1ifx=0),(kx,ifx=1or2),(k(5−x),ifx=3or4),(0,otherwise)
Find:
(i) k
(ii) the probability that you study exactly two hours,
(iii) the probability that you study at most two hours.
View SolutionIn a Poisson distribution if P(X=0)=P(X=1)=k, the value of k is
View SolutionA random variable X has the following probability distribution:
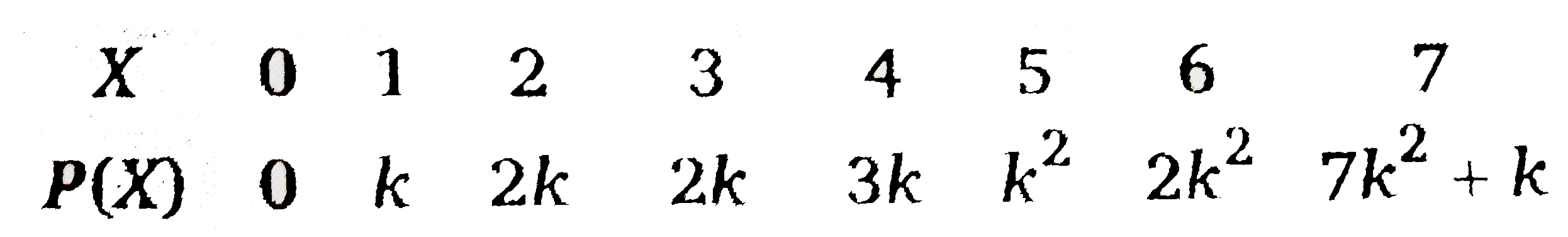
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionThe probability distribution for a random variable X is as follows:
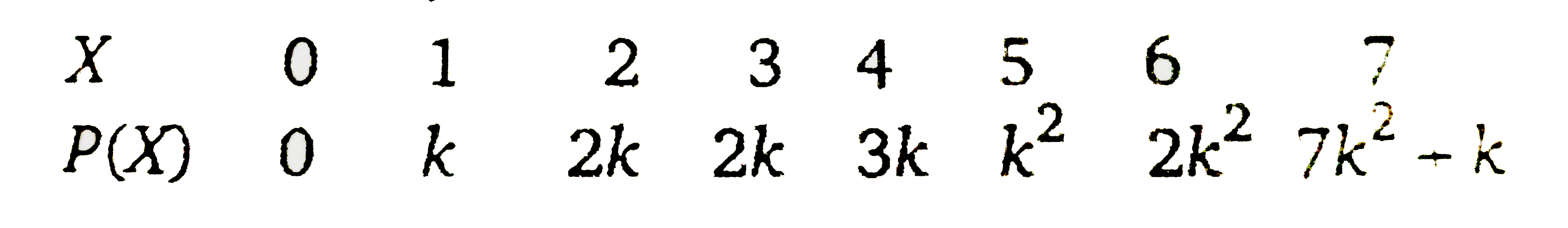
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
