The range of values of λ,λ>0 such that the angle θ between the pair of tangents drawn from (λ,0) to the circle x2+y2=4 lies in (π2,2π3) is
(4/√3,2√2)
(0,√2)
(1,2)
none of these
The correct Answer is:1
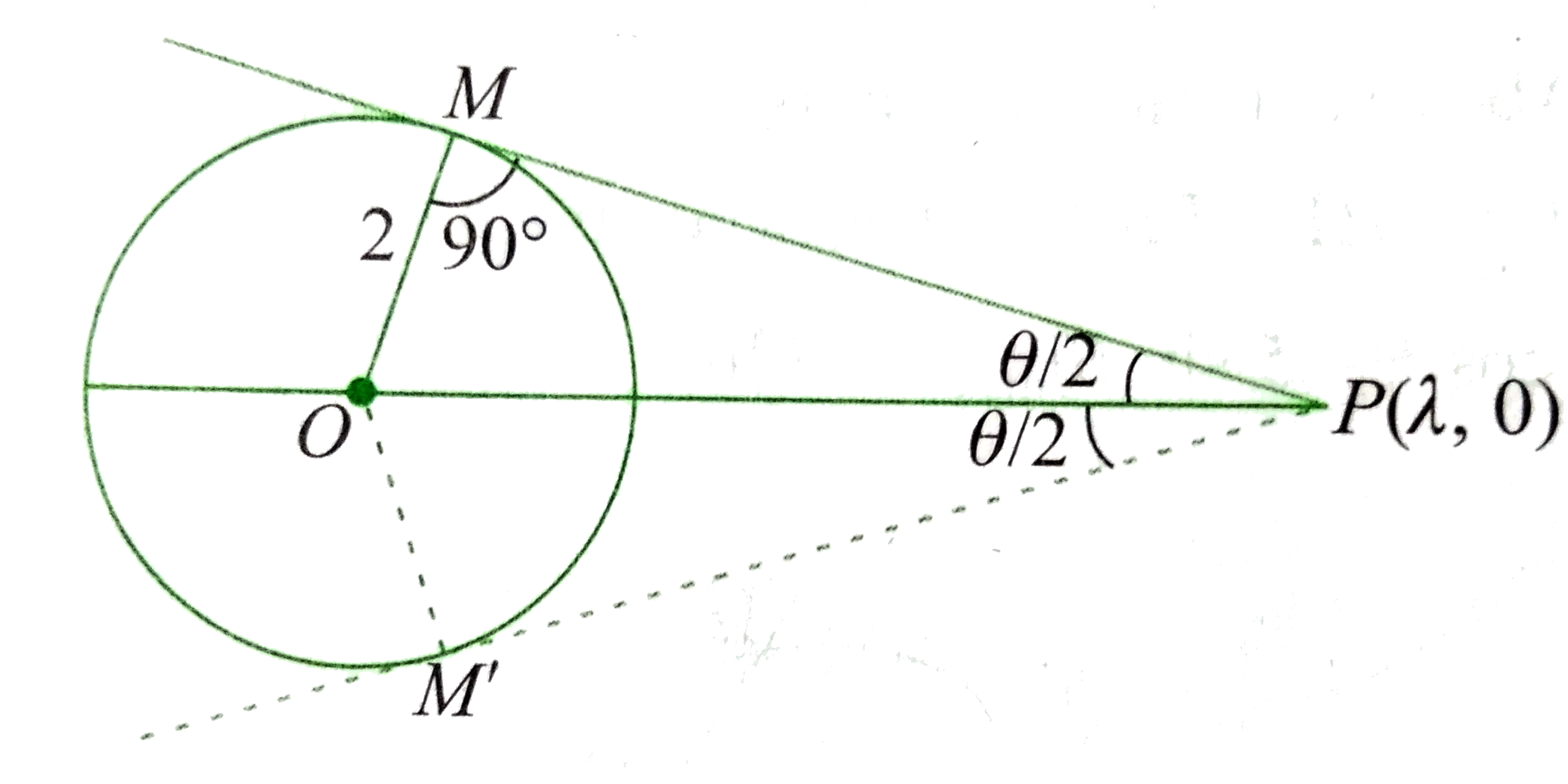
We have π2<θ<2π3,i.e., π4<θ2<π3
or 1√2<sin.θ2<√32
But sin.θ2=2λ or 1√2<2λ<√32
or 4√3<λ<2√2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
The range of values of λ,λ>0 such that the angle θ between the pair of tangents drawn from (λ,0) to the circle x2+y2=4 lies in (π2,2π3) is (a) (4√3,2√2) (b) (0,√2) (c) (1,2) (d) none of these
View SolutionThe range of values of a such that the angle θ between the pair of tangents drawn from (a,0) to the circle x2+y2=1 satisfies π2<θ<π is
View Solution
Knowledge Check
- Question 1 - Select One
The possible value of λ(λ>0) such that the angle between the pair of tangents from point (λ,0) to the circle x2+y2=4 lies in interval (π2,2π3) is
A(4√3,2√2)B(0,√2)C(1,2)D(−4√3,4√3)
The range of values of a such that the angle θ betweeen the pair of tangents drawn from (a,0) to the circle x2+y2=1 lies in (π3,π) is
View SolutionThe range of values of a such that the angle θ between the pair of tangents drawn from(a,0) to the circle x2+y2=1 satisfies π2<θ<π lies in
View SolutionThe exhaustive range of value of a such that the angle between the pair of tangents drawn from (a,a) to the circle x2+y2−2x−2y−6=0 lies in the range (π3,π) is
View SolutionIf the angle between tangents drawn to x2+y2+2gx+2fy+c=0 from (0,0) is π2, then
View SolutionAn infinite number of tangents can be drawn from (1,2) to the circle x2+y2−2x−4y+λ=0 . Then find the value of λ
View SolutionThe value of λ for which the equation x2−y2−x−λy−2=0 represent a pair of straight line, are
View SolutionIf the points (λ,−λ) lies inside the circle x2+y2−4x+2y−8=0, then find the range of λ.
View Solution

