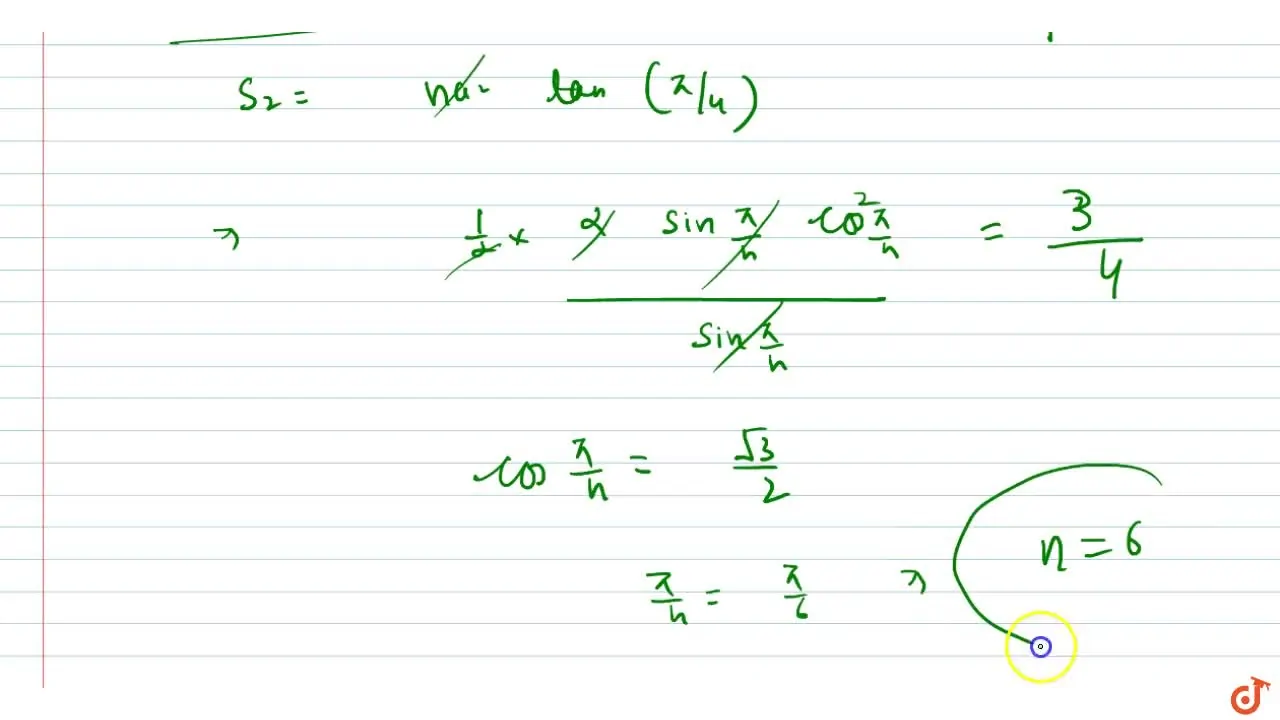The ratio of the area of a regular polygon of n sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of n is
Area of the polygon inscribed in a circle, (S1)=12na2sin(2πn)
Area of the polygon circumscribing the same circle, (S2)=na2tan(πn)
It is given that,
S1S2=34
∴12na2sin(2πn)na2tan(πn)=34
⇒12sin(2πn)tan(πn)=34
⇒12⋅2sin(πn)cos(πn)sin(πn)cos(πn)=34
⇒cos2(πn)=34
⇒cos(πn)=√32
⇒πn=π6
⇒n=6
∴ Sides of the polygon are 6.
Related Playlists
Similar Questions
The limit of the interior angle of a regular polygon of n sides as n→∞ is
View SolutionThe area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
View SolutionThe number of diagonals of a polygon of n sides is
View SolutionA regular polygon of n sides has 170 diagonals. Then n =
View SolutionA regular polygon has 20 sides. Find the number of diagonals of the polygon.
View SolutionProve that the area of a regular polygon hawing 2n sides, inscribed in a circle, is the geometric mean of the areas of the inscribed and circumscribed polygons of n sides.
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionThe area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionThe sum of the internal angles of a regular polygon is 1440∘. The number of sides is :
View Solution