A right angle is divided into three positive parts α,βandγ. Prove that for all possible divisions tanα+tanβ+tanγ>1+tanαtanβtanγ.
Step by step video & image solution for A right angle is divided into three positive parts alpha,betaa n dgammadot Prove that for all possible divisions t a nalpha+tanbeta+tangamma>1+tanalphatanbetatangammadot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A right angle is divided into three positive parts α,βandγ. Prove that for all possible divisions tanα+tanβ+tanγ>1+tanαtanβtanγ.
View SolutionIf a right angle be divided into three parts α,βandγ, prove that cotα=tanβ+tanγ1−tanβtanγ.
View SolutionIf a right angle be divided into three parts α,βandγ, prove that cotα=tanβ+tanγ1−tanβtanγ
View SolutionLet α,βandγ be some angles in the first quadrant satisfying tan(α+β)=158andcosecγ=178, then which of the following hold(s) good? (a) α+β+γ=π (b)cotα+tanβ+tanγ=tanαtanβtanγ (c)tanα+tanβ+tanγ=tanαtanβtanγ (d)tanαtanβ+tanβtanγ+tanγtanα=1
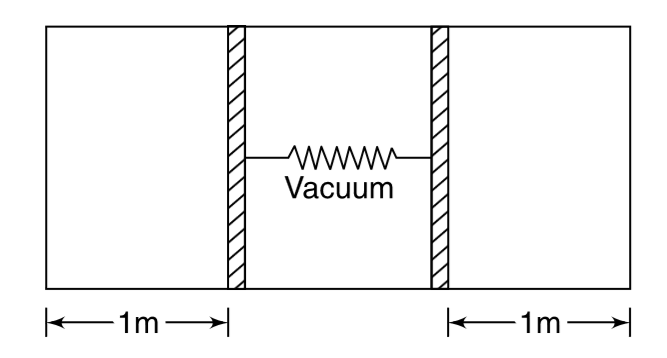
View SolutionA cylindrical container is divided into three parts by two tight fitting pistons. The pistons are connected by a spring. The region between the pistons is vacuum and the other two parts have same number of moles of an ideal gas. Initially, both the gas chambers are at temperature T0 and the spring is compressed by 1 m. Length of both gas chambers is 1 m in this position. Now the temperature of the left and right chambers are raised to 4T03 and 5T03 respectively. Find the final compression in the spring in equilibrium. Assume that the pistons slide without friction
View SolutionThe base of a triangle is divided into three equal parts. If θ1,θ2,θ3 be thw angles subtended by these parts at the vertex, then prove that
(cotθ1+cotθ2)(cotθ2+cotθ3)=4cosec2θ2
View SolutionIf P=x+1x and P(tanα)=2,P(tanβ)=2√2,P(cotγ)=4 where α,β,γ are acute angles and sum of all possible distinct values of α,β and γis given by mπn where m and n are coprime, then find the value of (m+n)
View SolutionThe base of a triangle is divided into three equal parts. If t1,t2,t3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1t1+1t2)(1t2+1t3)=4(1+1t22).
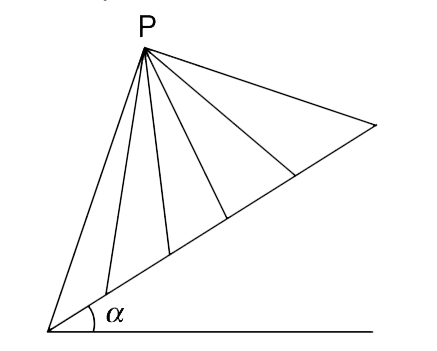
View Solution(a) Prove that bodies starting at the same time t=0 from the same point, and following frictionless slopes in different directions in the same vertical plane, all lie in a circle at any subsequent time.
(b) Using the above result do the following problem. A point P lies above an inclined plane of inclination angle α. P is joined to the plane at number of points by smooth wires, running in all possible directions. Small bodies (in shape of beads) are released from P along all the wires simultaneously. Which body will take least time to reach the plane.
View SolutionAn insulated cylindrical vessel is divided into three identical parts by two partitions 1 and 2. The left part contains O2 gas, the middle part has N2 and the third chamber has vacuum. The average molecular speed in oxygen chamber is V0 and that in nitrogen chamber is √87V0. Pressure of the gases in two chambers is same. Partition 1 is removed and the gases are allowed to mix. Now the stopper holding the partition 2 is removed and it slides to the right wall of the container, so that the mixture of gases occupy the entire volume of the container.
Find the average speed of O2 molecules now.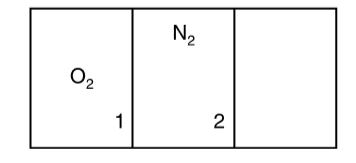
View Solution