The regression equation of x on y is 40x-18y = 214… (i)
The regression equation of y on x is 8x -10y +66 =0….. (ii)
Solving equations i and ii,
¯x=□
¯y=□
∴byx=□□
∴bxy=□□
∴r=□
The correct Answer is:13 , 17 , 45,920 0.6 , 4
To solve the problem, we need to find the values of ¯x, ¯y, byx, bxy, and r using the given regression equations.
Step 1: Solve the regression equations for ¯x and ¯y
We have the following regression equations:
1. 40x−18y=214 (Equation i)
2. 8x−10y+66=0 (Equation ii)
First, we can rearrange Equation ii:
8x−10y=−66(Rearranging)
Now we have:
1. 40x−18y=214
2. 8x−10y=−66
Step 2: Simplify the equations
Let's simplify both equations. We can divide the first equation by 2:
20x−9y=107(Equation i simplified)
And divide the second equation by 2:
4x−5y=−33(Equation ii simplified)
Step 3: Solve the system of equations
Now we can solve these two equations simultaneously. We can express x in terms of y from the second equation:
4x=5y−33⟹x=5y−334
Now substitute x in the first equation:
20(5y−334)−9y=107
Multiply through by 4 to eliminate the fraction:
20(5y−33)−36y=428
100y−660−36y=428
64y−660=428
64y=428+660
64y=1088
y=108864=17
Step 4: Find x
Now substitute y=17 back into the equation for x:
4x=5(17)−33
4x=85−33
4x=52⟹x=524=13
Thus, we have:
¯x=13,¯y=17
Step 5: Find the regression coefficients
Next, we find the regression coefficients bxy and byx.
For bxy (from equation i):
The regression equation can be written as:
x−¯x=bxy(y−¯y)
Rearranging gives:
40x−18y=214⟹x−13=1840(y−17)
Thus,
bxy=1840=920
For byx (from equation ii):
The regression equation can be written as:
y−¯y=byx(x−¯x)
Rearranging gives:
8x−10y+66=0⟹y−17=810(x−13)
Thus,
byx=810=45
Step 6: Find the correlation coefficient r
The correlation coefficient r can be calculated using:
r=√byx⋅bxy=√(45)⋅(920)
Calculating this gives:
r=√36100=610=0.6
Summary of Results
- ¯x=13
- ¯y=17
- byx=45
- bxy=920
- r=0.6
1. 40x−18y=214 (Equation i)
2. 8x−10y+66=0 (Equation ii)
8x−10y=−66(Rearranging)
1. 40x−18y=214
2. 8x−10y=−66
20x−9y=107(Equation i simplified)
4x−5y=−33(Equation ii simplified)
4x=5y−33⟹x=5y−334
20(5y−334)−9y=107
20(5y−33)−36y=428
100y−660−36y=428
64y−660=428
64y=428+660
64y=1088
y=108864=17
4x=5(17)−33
4x=85−33
4x=52⟹x=524=13
¯x=13,¯y=17
The regression equation can be written as:
x−¯x=bxy(y−¯y)
Rearranging gives:
40x−18y=214⟹x−13=1840(y−17)
Thus,
bxy=1840=920
The regression equation can be written as:
y−¯y=byx(x−¯x)
Rearranging gives:
8x−10y+66=0⟹y−17=810(x−13)
Thus,
byx=810=45
r=√byx⋅bxy=√(45)⋅(920)
Calculating this gives:
r=√36100=610=0.6
- ¯x=13
- ¯y=17
- byx=45
- bxy=920
- r=0.6
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 4. TIME SERIES (I) Choose the correct alternative.)
5 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 4. TIME SERIES (II) Fill in the blanks
5 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 3. LINEAR REGRESSION (IV.Answer the following:)
15 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
In the regression equation of X on Y
AX is independent and Y is dependent.BY is independent and X is dependent.CBoth X and Y are independent.DBoth X and Y are dependent.Regression equation of yon is 8x-10y+66=0 σx=3. Hence cov(x,y) is equal to
A11,25B7.2C2,4DNone of theseIf the regression equation x on y is 3x+2y=26 then bxy equals to
A3/2B2/3C−3/2D−2/3
Mean of x= 25
Mean of y =20
σx=4
σy=3
r=0.5
byx=□
bxy=□
When x = 10
y−□=□(10−□)
∴y=□
View Solution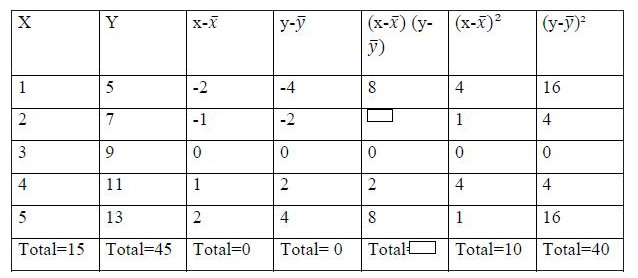
Mean of x=¯x=□
Mean y=¯y=□
bxy=□□
byx=□□
Regression equation of x on y is x−¯x=bxy(y−¯y)
∴ Regression equation of x on y is □
Regression equation of y on x is y−¯y=byx(x−¯x)
∴ Regression equation of y on x is □
View Solution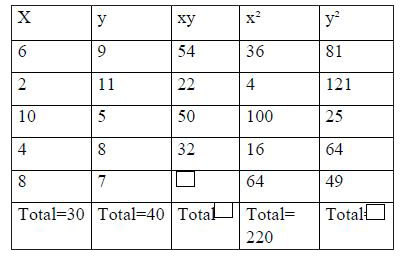
bxy=□□
byx=□□
∴ Regression equation of x on y is □
∴ Regression equation of y on x is □
View SolutionIf the regression equations are 8x–10y+66=0 and 40x–18y=214, the mean value of y is…..
View SolutionComplete the following activity to solve simultaneous equations :
4x+3y=18 ...(1)5x−3y=9 ...(2)
Adding equations (1) and (2) , +4x+3y=18 ...(1)5x−3y=9 ...(2)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯□x =□
∴X=□□ ∴X=□
Substituting x = 3 in equation (1) ,
4×□+3y=18 ∴3y=18−□ ∴3y=□
∴y=2
(x,y ) = (□,□) is the solution
View Solution
