The seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression. Solution in Kannada
The correct Answer is:The required sequence 2, 5, 8 .....
Step by step video, text & image solution for The seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ZEN ADDITIONAL QUESTIONS (LONG-ANSWER [LA] TYPE - QUESTIONS)
14 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ZEN ADDITIONAL QUESTIONS (HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS)
4 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ZEN ADDITIONAL QUESTIONS (SHORT-ANSWER [SA] TYPE 1 - QUESTIONS)
24 Videos
- AREA RELATED TO CIRCLES BOOK - ZEN PUBLICATIONCHAPTER - AREA RELATED TO CIRCLES EXERCISE - ADDITIONAL QUESTIONS (HIGHER ORDER THINKING SKILLS)
7 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
Similar Questions
If the sum of n terms of A.P. is 12(3n2+7n) , find its nth term and write its 25th term.
View SolutionIf m times the mth term of an A.P. is equal ton times the nth term and m≠n, show that (m+n)th term is zero.
View SolutionWrite the nth term of the AP:
a] 13,8,3,−2,…..
b] √2,3√2,5√2,…..
c] 121,117,113,…..
d] 34,54,74,….
e] −15,−10,−5,0,….....
View SolutionFind the area of the shaded region portion in the given figure if E is the midpoint of AB,AGE and BEF are quadrants, and DOC is a semicircle.

View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
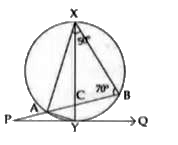
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometic progression colncide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe seventh term of an Arithmetic progression is four times its second term and twelfth term is 2 more than three times of its fourth term.Find the progression.
View SolutionIf seven times of 7th term of an Arithmetic Progression is euqal to the 11 times of 11th term of it, then find the 18th term of that Arithmetic Progression.
View SolutionThe seventh term of an arithmetic progression is four times itss second term and twelth term is 2 more than three times of its fourth term. Find the progression.
View SolutionIn an arithmetic progression sixth term is one more than twice the thrid term. Tha sum of the fourth and fifth terms is five times the secon term. Find the tenth term of the arithmatic progression.
View SolutionThe first, second and seventh terms of an arithmetic progression (all the terms are distinct) are in geometric progression and the sum of these three terms is 93. Then, the fourth term of this geometric progression is
View SolutionIn an arithmetic progression, thrice the second term is equivalent to eighth term and the sum of fourth term and the seventh term is 9 greater than the ninth term. Find the AP.
View SolutionThe sum of the fourth and eighth terms of an arithmetic progression is 24 and the sum of the sixth and tenth terms is 44. Find the first three terms of the Arithmetic progression.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe third term of an arithmetical progression is 7, and the seventh term is 2 more than 3 times the third term. Find the first term, the common difference and the sum of the first 20 terms.
View Solution
