The shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60∘ to 45∘. If the height of the tower is 5(3+√3)m, then what is x equal to ?
8 m
10 m
12 m
15 m
To solve the problem, we need to find the length x of the shadow of the tower when the angle of elevation of the sun changes from 60∘ to 45∘. The height of the tower is given as 5(3+√3) meters.
Step 1: Calculate the height of the tower
The height h of the tower is:
h=5(3+√3) meters
Step 2: Find the length of the shadow when the angle of elevation is 60∘
Using the tangent function:
tan(60∘)=heightshadow length at 60∘
Let the shadow length at 60∘ be L1:
√3=hL1
Rearranging gives:
L1=h√3=5(3+√3)√3
Simplifying L1:
L1=15+5√3√3=5√3+5
Step 3: Find the length of the shadow when the angle of elevation is 45∘
Using the tangent function again:
tan(45∘)=heightshadow length at 45∘
Let the shadow length at 45∘ be L2:
1=hL2
Rearranging gives:
L2=h=5(3+√3)
Step 4: Find the difference in shadow lengths
The difference in shadow lengths when the angle changes from 60∘ to 45∘ is:
x=L2−L1
Substituting the values:
x=5(3+√3)−(5√3+5)
Simplifying:
x=15+5√3−5√3−5=15−5=10
Conclusion
Thus, the value of x is:
10 meters
The height h of the tower is:
h=5(3+√3) meters
Using the tangent function:
tan(60∘)=heightshadow length at 60∘
Let the shadow length at 60∘ be L1:
√3=hL1
Rearranging gives:
L1=h√3=5(3+√3)√3
Simplifying L1:
L1=15+5√3√3=5√3+5
Using the tangent function again:
tan(45∘)=heightshadow length at 45∘
Let the shadow length at 45∘ be L2:
1=hL2
Rearranging gives:
L2=h=5(3+√3)
The difference in shadow lengths when the angle changes from 60∘ to 45∘ is:
x=L2−L1
Substituting the values:
x=5(3+√3)−(5√3+5)
Simplifying:
x=15+5√3−5√3−5=15−5=10
Thus, the value of x is:
10 meters
Topper's Solved these Questions
Similar Questions
The shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from 45∘ to 30∘. Find the height of the tower.
View SolutionThe shadow of a standing tower of height 2575 m is found to be 50 m longer when the sun’s elevation changes from 60∘ to x∘. Find the measure of X
View Solution
Knowledge Check
The shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
A15√3 metresB15(3+√3) metresC15(3−√3) metresD12(3+√3) metresThe shadow of a tower on ground level is increased by 30 m, when the angle of depression by the sun changes from 60∘ to 30∘. The height of the tower is?
A. 12√3 m
B. 17√3 m
C. 16√3m
D. 15√3 mABBCCDDAThe shadow of a tower standing on a level plane is found to be 50 m longer when the Sun's elevation is 30∘ than when it is 60∘. The height of the tower is
AA. 25 mBB. 25√3mCC. 50mDD. None of these
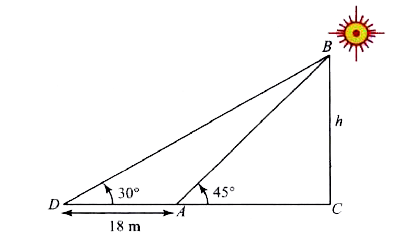
The shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
View SolutionThe shadow of a tower standing on a level plane is found to be 50 m longer when the Sun's elevation is 30∘ than when it is 60∘ What is the height of the tower ?
View SolutionThe shadow of a tower is found to be 60 ft. longer when the sun's altitude has become 60∘ from 30∘. The height of the tower from the ground is
View SolutionThe shadow of a tower is √3 times its height .Then the angle of elevation of the top of the tower is
View SolutionThe shadow of a tower is found to be 60 m shorter when the Sun’s altitude change from 30∘ to 60∘.The height of the power from the ground is approximately
View Solution
