The solution set of x2+2≤3x≤2x2−5, is
ϕ
[1,2]
(−∞,−1]∪[5/2,∞)
none of these
The correct Answer is:A
To solve the inequality x2+2≤3x≤2x2−5, we will break it down into two parts and solve each inequality separately.
Step 1: Solve x2+2≤3x
1. Rearrange the inequality:
x2−3x+2≤0
2. Factor the quadratic:
(x−1)(x−2)≤0
3. Determine the critical points:
The critical points are x=1 and x=2.
4. Test intervals:
- For x<1 (e.g., x=0): (0−1)(0−2)=2>0 (not in solution set)
- For 1≤x≤2 (e.g., x=1.5): (1.5−1)(1.5−2)=−0.25<0 (in solution set)
- For x>2 (e.g., x=3): (3−1)(3−2)=2>0 (not in solution set)
5. Conclusion for this part:
1≤x≤2
Step 2: Solve 3x≤2x2−5
1. Rearrange the inequality:
2x2−3x−5≥0
2. Factor the quadratic:
To factor, we can use the quadratic formula to find the roots:
x=−b±√b2−4ac2a=3±√(−3)2−4⋅2⋅(−5)2⋅2
=3±√9+404=3±74
Thus, the roots are:
x=104=52andx=−44=−1
3. Rewrite the inequality using the roots:
(x−52)(x+1)≥0
4. Determine the intervals:
- For x<−1 (e.g., x=−2): (−2−52)(−2+1)=positive (in solution set)
- For −1<x<52 (e.g., x=0): (0−52)(0+1)=negative (not in solution set)
- For x>52 (e.g., x=3): (3−52)(3+1)=positive (in solution set)
5. Conclusion for this part:
x≤−1orx≥52
Step 3: Solve x2+2≤2x2−5
1. Rearrange the inequality:
x2−7≤0
2. Factor:
(x−√7)(x+√7)≤0
3. Determine the critical points:
The critical points are x=−√7 and x=√7.
4. Test intervals:
- For x<−√7: (e.g., x=−3): positive (not in solution set)
- For −√7≤x≤√7: (e.g., x=0): negative (in solution set)
- For x>√7: positive (not in solution set)
5. Conclusion for this part:
−√7≤x≤√7
Final Step: Combine the results
1. From the first inequality, we have 1≤x≤2.
2. From the second inequality, we have x≤−1 or x≥52.
3. From the third inequality, we have −√7≤x≤√7.
Conclusion:
The solution set is the intersection of all three parts. Since there are no common values in the ranges (1,2), (−∞,−1)∪(52,∞), and (−√7,√7), we conclude that there is no solution.
x2−3x+2≤0
(x−1)(x−2)≤0
The critical points are x=1 and x=2.
- For x<1 (e.g., x=0): (0−1)(0−2)=2>0 (not in solution set)
- For 1≤x≤2 (e.g., x=1.5): (1.5−1)(1.5−2)=−0.25<0 (in solution set)
- For x>2 (e.g., x=3): (3−1)(3−2)=2>0 (not in solution set)
1≤x≤2
2x2−3x−5≥0
To factor, we can use the quadratic formula to find the roots:
x=−b±√b2−4ac2a=3±√(−3)2−4⋅2⋅(−5)2⋅2
=3±√9+404=3±74
Thus, the roots are:
x=104=52andx=−44=−1
(x−52)(x+1)≥0
- For x<−1 (e.g., x=−2): (−2−52)(−2+1)=positive (in solution set)
- For −1<x<52 (e.g., x=0): (0−52)(0+1)=negative (not in solution set)
- For x>52 (e.g., x=3): (3−52)(3+1)=positive (in solution set)
x≤−1orx≥52
x2−7≤0
(x−√7)(x+√7)≤0
The critical points are x=−√7 and x=√7.
- For x<−√7: (e.g., x=−3): positive (not in solution set)
- For −√7≤x≤√7: (e.g., x=0): negative (in solution set)
- For x>√7: positive (not in solution set)
−√7≤x≤√7
2. From the second inequality, we have x≤−1 or x≥52.
3. From the third inequality, we have −√7≤x≤√7.
Topper's Solved these Questions
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Section I - Solved Mcqs
20 Videos
- ALGEBRA OF VECTORSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test
30 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
Similar Questions
Knowledge Check
The solution set of 3x5+2<x+4≤x2+5,x∈R on the number line is:
A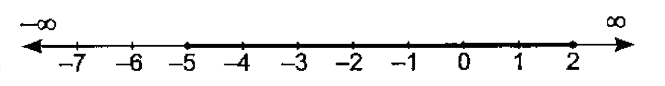 B
B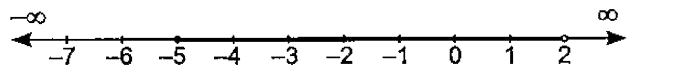 C
C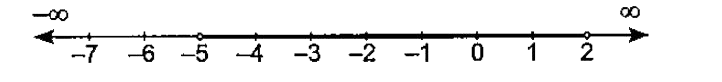 D
D
Assertion: The solution set of 2x−3≤x+1≤4x+7,x∈N is {1, 2, 3,4} .
Reason: If the solution of a linear inequation is x>2,x∈R then on the number line, it is represented as
 ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correct
ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correctThe solution set of −2+10x≤13x+10<24+10x,x∈Z is
A{−4,−3,−2,−1,0,1,2,3,4,5}B{−4,−3,−2,−1,0,1,2,3,4}C{−3,−2,−1,0,1,2,3,4}D{−3,−2,−1,0,1,2,3,4,5}
