The stiffness of a beam of rectangular cross-section varies as the product of the breadth and square of the depth. What must be the breadth of the stiffest beam that can be cut from a leg of diameter 'd'?
The correct Answer is:width=d/sqrt3" metre,
To solve the problem, we need to find the breadth B of the stiffest beam that can be cut from a leg of diameter d. The stiffness I of the beam is given to vary as the product of the breadth and the square of the depth.
Step 1: Define the variables
Let:
- B = breadth of the beam
- H = depth of the beam
- d = diameter of the leg
Step 2: Relate the breadth and depth to the diameter
Since the beam is rectangular and fits inside a circular leg of diameter d, we can use the Pythagorean theorem:
B2+H2=d2
From this, we can express H in terms of B:
H2=d2−B2
Step 3: Express the stiffness
The stiffness I is proportional to the breadth and the square of the depth:
I=kBH2
Substituting H2 from the previous step:
I=kB(d2−B2)
This simplifies to:
I=k(Bd2−B3)
Step 4: Differentiate the stiffness with respect to breadth
To find the maximum stiffness, we differentiate I with respect to B:
dIdB=k(d2−3B2)
Step 5: Set the derivative to zero to find critical points
To find the critical points, set the derivative equal to zero:
d2−3B2=0
Solving for B:
3B2=d2⇒B2=d23⇒B=d√3
Step 6: Verify that this is a maximum
To confirm that this critical point gives a maximum, we can find the second derivative:
d2IdB2=−6kB
Since k>0 and B>0, we have:
d2IdB2<0
This indicates that the stiffness is maximized at B=d√3.
Final Answer
The breadth of the stiffest beam that can be cut from a leg of diameter d is:
B=d√3
Let:
- B = breadth of the beam
- H = depth of the beam
- d = diameter of the leg
Since the beam is rectangular and fits inside a circular leg of diameter d, we can use the Pythagorean theorem:
B2+H2=d2
From this, we can express H in terms of B:
H2=d2−B2
The stiffness I is proportional to the breadth and the square of the depth:
I=kBH2
Substituting H2 from the previous step:
I=kB(d2−B2)
This simplifies to:
I=k(Bd2−B3)
To find the maximum stiffness, we differentiate I with respect to B:
dIdB=k(d2−3B2)
To find the critical points, set the derivative equal to zero:
d2−3B2=0
Solving for B:
3B2=d2⇒B2=d23⇒B=d√3
To confirm that this critical point gives a maximum, we can find the second derivative:
d2IdB2=−6kB
Since k>0 and B>0, we have:
d2IdB2<0
This indicates that the stiffness is maximized at B=d√3.
The breadth of the stiffest beam that can be cut from a leg of diameter d is:
B=d√3
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6h (multiple Choice Questions)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6i (multiple Choice Questions)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6f
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a.
View SolutionThe cost of painting a rectangular metal sheet is square of its area. If the length and breadth of the rectangle are 2xy and 3x2y, find the cost. Given that area of a rectangle is the product of its length and breadth.
View Solution
Knowledge Check
a thin slice is cut from a bagel, creating the cross - section represented below . The diameter of the bagel is 144 mm and the width from the inner edge of the bagel to the outer edge is uniformly 56 mm. Which of the following is closest to the area , in square millimeters , of the shaded empty space inside the cross -section of the bagel ?
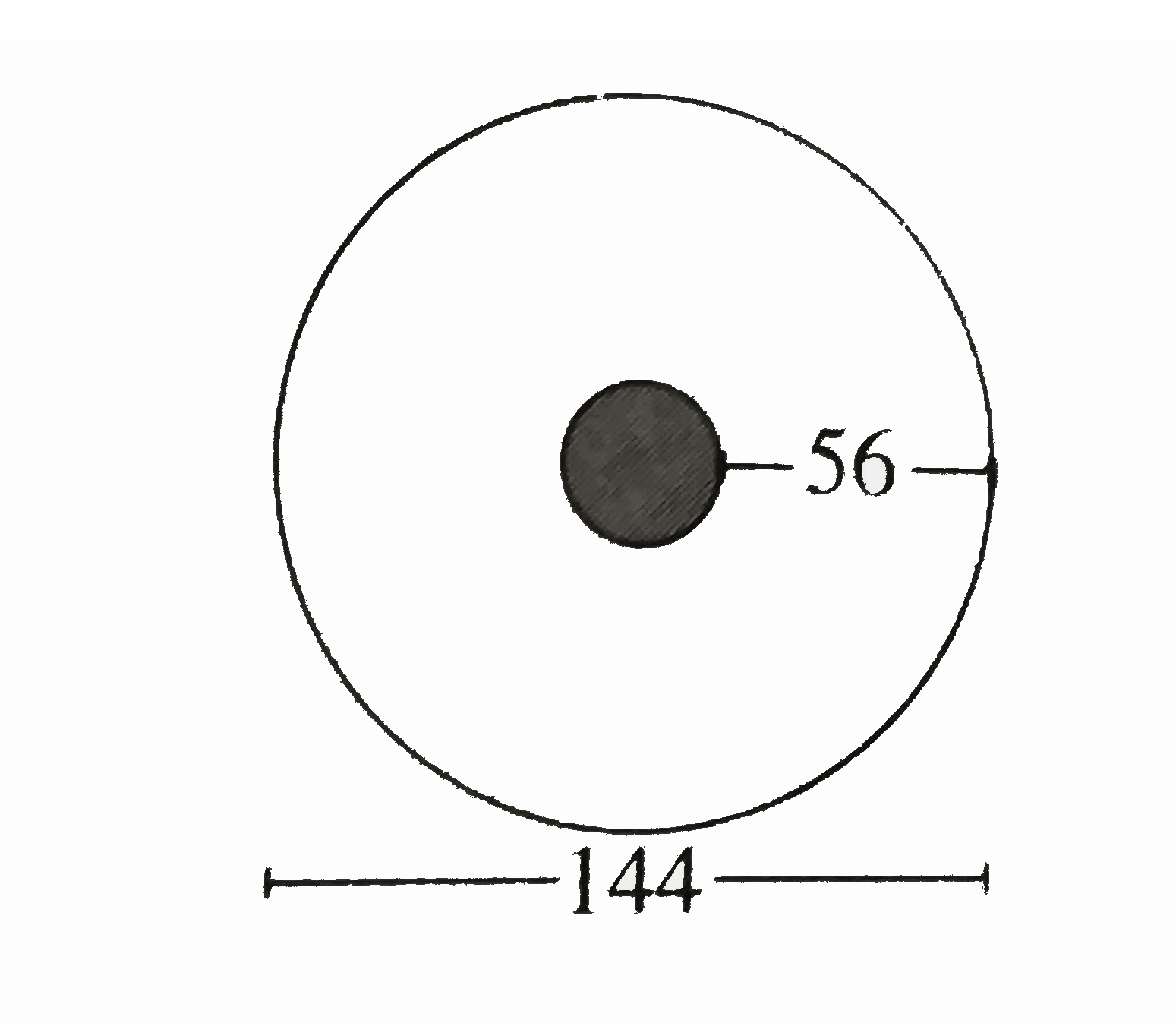 A100B450C800D3,200
A100B450C800D3,200
Write the following using numbers, literals and signs of basic operations State what each letter represents: The diameter of a circle is twice its radius. The area of a rectangle is the product of its length and breadth. The selling price equals the sum of the cost price and the profit. The total amount equals the sum of the principal and the interest. The perimeter of a rectangle is two times the sum of its length and breadth. The perimeter of a square is four times its side.
View SolutionA square sheet of side 5cm is cut out from a rectangular piece of an aluminium sheet of length 9cm and breadth 6cm. What is the area of the aluminium sheet left over?
View SolutionA square sheet of 2cm is cut from each corner of a rectangular piece of aluminium sheet of length 12cm and breadth 8cm. Find the area of the left over aluminium sheet.
View SolutionElectrons in a beam are accelerated from rest through a potential difference ΔV. The beam enters an experimental chamber through a small hole. As shown in Fig. 1.35, the electron velocity vector lie within a narrow cone of half angle ϕ oriented along the beam axis. We wish to use a uniform magnetic field directed parallel to the axis to focus the beam, so that all of the electrons can pass through a small exit port on the opposite side of the chamber after they travel the length d of the chamber. What is the required magnitude of the magnitude field?

View SolutionA rectangular cardboard sheet has length 32 cm and breadth 26 cm. The four squares each of side 3 cm are cut from the corners of the sheet and the sides are folded to make a rectanguler container. Find the capacity of the container.
View SolutionA rectangular card-board sheet has length 32cm and breadth 26cm. Squares each of side 3cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
View SolutionA rod of glass (μ=1.5) and of square cross section is bent into the shape shown in the figure. A parallel beam of light falls on the plane flat surface A as shown in the figure. If d is the width of a side and R is the radius of circular arc then for what maximum value of dR light entering the glass slab through surface A emerges from the glass through B
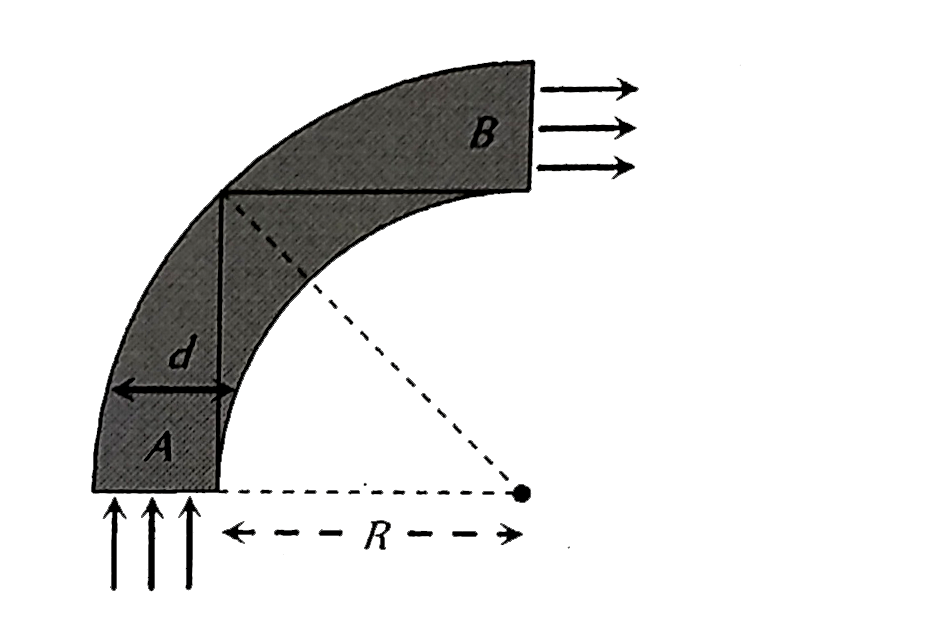
View Solution
