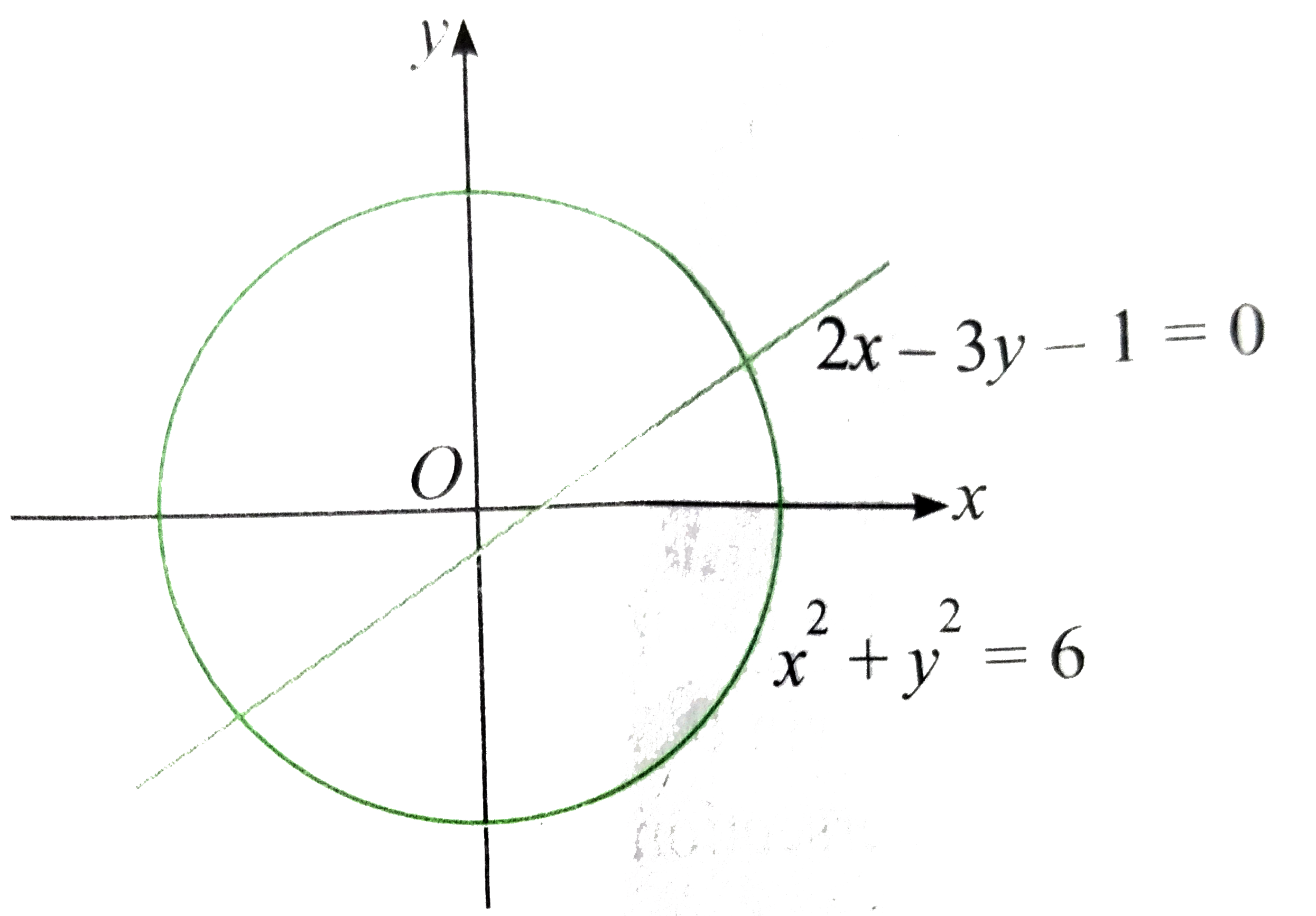
The straight line 2x-3y = 1 divides the circular region x^2+ y^2 le6 i

Let the straight line x = b divide the area enclosed by $y = {(1 - x)}^{2}, y = 0$ and $x = 0$ into two parts $R_{1} (0 \leq x \leq b)$ and $R_{2} (b \leq x \leq 1)$ such that $R_{1} - R_{2} = \frac{1}{4}$ . Then b equals
A $\frac{3}{4}$
B $\frac{1}{2}$
C $\frac{1}{3}$
D $\frac{1}{4}$
If the straight line x=b divide the area enclosed by $y = {(1 - x)}^{2}, y = 0 and x = 0 into two parts R_{1} (0 \leq x \leq b) and R_{2} (b \leq x \leq 1) such that R_{1} - R_{2} = \frac{1}{4} .$ Then, b equals
A $\frac{3}{4}$
B $\frac{1}{2}$
C $\frac{1}{3}$
D $\frac{1}{4}$
The parabolas $y^{2} = 4 x and x^{2} = 4 y$ divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If $S_{1}, S_{2}, S_{3}$ are the areas of these parts numbered from top to bottom, respectively, then
A $S_{1} : S_{2} \equiv 1 : 1$
B $S_{2} : S_{3} \equiv 1 : 2$
C $S_{1} : S_{3} \equiv 1 : 1$
D $S_{1} : (S_{1} + S_{2}) = 1 : 2$

The straight line 2x-3y = 1 divides the circular region $x^{2} + y^{2} \leq 6$ into two parts. If S = { $(2, \frac{3}{4}), (\frac{5}{2}, \frac{3}{4}), (\frac{1}{4}, - \frac{1}{4}), (\frac{1}{8}, \frac{1}{4})$ }, then the number of point(s) in S lying inside the smaller part is