The straight line x4+y3=1 intersects the ellipse x216+y29=1 at two points A and B, there is a point P on this ellipse such that the area of ΔPAB is equal to 6(√2−1). Then the number of such points (P) is/are
A
0
B
1
C
2
D
3
Text Solution
The correct Answer is:D
Let the perpendicular distance of P from the line be h,
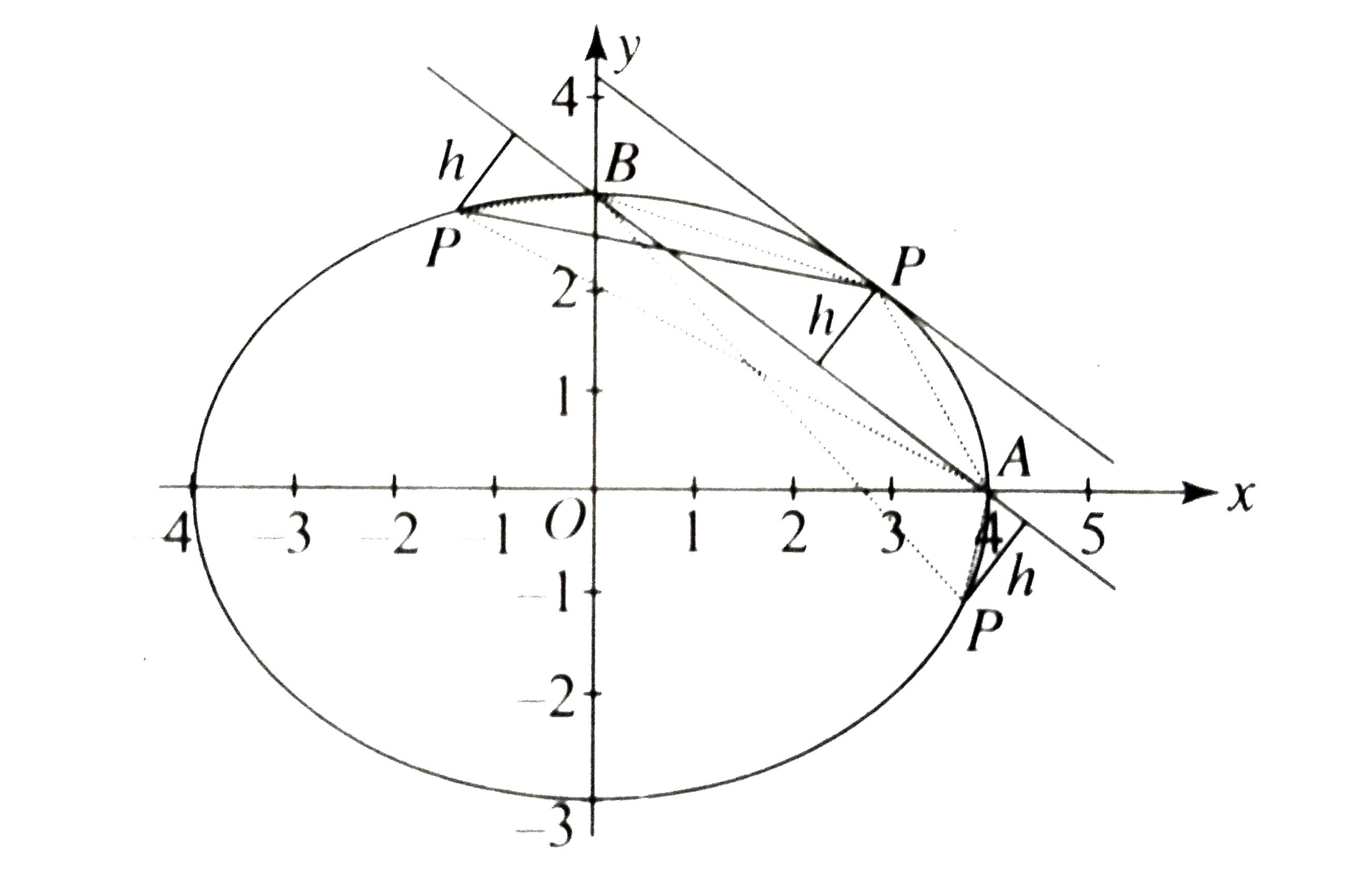
∴12×h×5=6(√2−1)
∴h=125(√2−1)
Also tangent parallel to the given line is 4y+3x=12√2
Its distance from the line 4y+3x=12 is h=125(√2−1) Hence there are three points as shown in the figure.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The line y=bt meets the ellipse x2a2+y2b2=1 in real points if
A|t|≤1B|t|>1C|t|<3D|t|<4The line y=2t2 meets the ellipse x29+y24=1 in real points if
A|t|≤1B|t|≥1C|t|<3DNone of these
If the line y=x+√3 touches the ellipse x24+y21=1 then the point of contact is
View SolutionIf the line y=x+√3 touches the ellipse x24+y21=1 then the point of contact is
View SolutionIf 3x+4y=12 intersect the ellipse x225+y216=1 at P and Q , then point of intersection of tangents at P and Q.
View SolutionThe line x+2y=1 cuts the ellipse x2+4y2=1 1 at two distinct points A and B. Point C is on the ellipse such that area of triangle ABC is maximum, then find point C.
View SolutionThe line x+2y=1 cuts the ellipse x2+4y2=1 1 at two distinct points A and B. Point C is on the ellipse such that area of triangle ABC is maximum, then find point C.
View SolutionThe line 2x+y=3 intersects the ellipse 4x2+y2=5 at two points. The point of intersection of the tangents to the ellipse at these point is
View Solution
