The table below gives an incomplete frequency distribution with two missing frequencies f1andf2
∣∣
∣
∣
∣
∣
∣
∣∣Value of xFrequency0f11f2243443∣∣
∣
∣
∣
∣
∣
∣∣
The total frequency is 18 and the arithmetic mean of x is 2.
What is the standard deviation?
√52
√53
43
169
The correct Answer is:C
To solve the problem, we need to find the missing frequencies f1 and f2 and then calculate the standard deviation of the distribution. Let's break this down step by step.
Step 1: Set Up the Frequency Distribution Table
We have the following values and frequencies:
| Value of x | Frequency |
|------------|-----------|
| 0 | f1 |
| 1 | f2 |
| 2 | 4 |
| 3 | 4 |
| 4 | 3 |
Step 2: Write the Total Frequency Equation
The total frequency is given as 18. Therefore, we can write the equation:
f1+f2+4+4+3=18
This simplifies to:
f1+f2+11=18
Thus, we have:
f1+f2=7(Equation 1)
Step 3: Calculate the Mean
The arithmetic mean ¯x is given as 2. The formula for the mean is:
¯x=∑(x⋅f)∑f
We need to calculate ∑(x⋅f):
∑(x⋅f)=0⋅f1+1⋅f2+2⋅4+3⋅4+4⋅3
This simplifies to:
∑(x⋅f)=0+f2+8+12+12=f2+32
Now substituting into the mean formula:
2=f2+3218
Multiplying both sides by 18 gives:
36=f2+32
Thus, we can solve for f2:
f2=36−32=4(Equation 2)
Step 4: Solve for f1
Now we can substitute f2 back into Equation 1:
f1+4=7
This gives us:
f1=7−4=3
Step 5: Complete the Frequency Distribution Table
Now we have:
f1=3,f2=4
So the complete frequency distribution table is:
| Value of x | Frequency |
|------------|-----------|
| 0 | 3 |
| 1 | 4 |
| 2 | 4 |
| 3 | 4 |
| 4 | 3 |
Step 6: Calculate the Standard Deviation
To find the standard deviation, we first need to calculate the mean again, which we already found to be 2.
Now we calculate ∑(x−¯x)2f:
∑(x−2)2f=(0−2)2⋅3+(1−2)2⋅4+(2−2)2⋅4+(3−2)2⋅4+(4−2)2⋅3
Calculating each term:
- For x=0: (0−2)2⋅3=4⋅3=12
- For x=1: (1−2)2⋅4=1⋅4=4
- For x=2: (2−2)2⋅4=0⋅4=0
- For x=3: (3−2)2⋅4=1⋅4=4
- For x=4: (4−2)2⋅3=4⋅3=12
Now summing these:
∑(x−2)2f=12+4+0+4+12=32
Step 7: Calculate the Variance and Standard Deviation
The variance σ2 is given by:
σ2=∑(x−¯x)2fn
Where n=18:
σ2=3218=169
Thus, the standard deviation σ is:
σ=√169=43
Final Answer
The standard deviation is 43.
We have the following values and frequencies:
|------------|-----------|
| 0 | f1 |
| 1 | f2 |
| 2 | 4 |
| 3 | 4 |
| 4 | 3 |
The total frequency is given as 18. Therefore, we can write the equation:
f1+f2+4+4+3=18
This simplifies to:
f1+f2+11=18
Thus, we have:
f1+f2=7(Equation 1)
The arithmetic mean ¯x is given as 2. The formula for the mean is:
¯x=∑(x⋅f)∑f
We need to calculate ∑(x⋅f):
∑(x⋅f)=0⋅f1+1⋅f2+2⋅4+3⋅4+4⋅3
This simplifies to:
∑(x⋅f)=0+f2+8+12+12=f2+32
Now substituting into the mean formula:
2=f2+3218
Multiplying both sides by 18 gives:
36=f2+32
Thus, we can solve for f2:
f2=36−32=4(Equation 2)
Now we can substitute f2 back into Equation 1:
f1+4=7
This gives us:
f1=7−4=3
Now we have:
f1=3,f2=4
So the complete frequency distribution table is:
|------------|-----------|
| 0 | 3 |
| 1 | 4 |
| 2 | 4 |
| 3 | 4 |
| 4 | 3 |
To find the standard deviation, we first need to calculate the mean again, which we already found to be 2.
∑(x−2)2f=(0−2)2⋅3+(1−2)2⋅4+(2−2)2⋅4+(3−2)2⋅4+(4−2)2⋅3
Calculating each term:
- For x=0: (0−2)2⋅3=4⋅3=12
- For x=1: (1−2)2⋅4=1⋅4=4
- For x=2: (2−2)2⋅4=0⋅4=0
- For x=3: (3−2)2⋅4=1⋅4=4
- For x=4: (4−2)2⋅3=4⋅3=12
∑(x−2)2f=12+4+0+4+12=32
The variance σ2 is given by:
σ2=∑(x−¯x)2fn
Where n=18:
σ2=3218=169
Thus, the standard deviation σ is:
σ=√169=43
The standard deviation is 43.
Topper's Solved these Questions
- BOOK - NDA PREVIOUS YEARSCHAPTER - SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM EXERCISE - MCQ271videos
SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM
- BOOK - NDA PREVIOUS YEARSCHAPTER - TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONSEXERCISE - MCQ238videos
TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The table below gives an incomplete frequency distribution with two missing frequencies f1andf2
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Value of xFrequency0f11f2243443∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
The total frequency is 18 and the arithmetic mean of x is 2.
What is the value of f2?A4B3C2D1 - Question 2 - Select One
The table below gives an incomplete frequency distribution with two missing frequencies f1andf2
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Value of xFrequency0f11f2243443∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
The total frequency is 18 and the arithmetic mean of x is 2.
What is the coefficient of variance ?A2003B50√59C600√5D150 - Question 3 - Select One
Let f1 be the frequency
Af1−f2=f3Bf2−f1=f3Cf3=12(f1+f2)Df1+f2=f3.
Observe the following data :

If the above data has mean = 50 , then missing frequencies f1andf2 areView SolutionThe mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies f1 and f2:
View SolutionThe mean of the following frequency distribution is 57.6 and the number of observation is 50. Find the missing frequency f1&f2
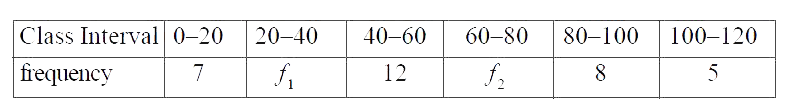 View Solution
View SolutionThe total number of observations in the following distribution table is 120 and their mean is 50. Find the value of missing frequencies f1andf2 :
 View Solution
View SolutionConsider the following frequency distribution:

What are the values of f1, and f2, respectively?View Solution



