The three planes, determine a rectangular parallelopiped which has ………. Of rectangular faces.
Three points.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - Objective type Questions13videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Objective type13videos
CONIC SECTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - FILLERS4videos
LIMITS AND DERIVATIVES
Similar Questions
Knowledge Check
- Question 1 - Select One
A prism which has only five rectangular faces is called a
Atriangular prismBrectangular prismChexagonal prismDpentagonal prism - Question 2 - Select One
The ratio of the length and breadth of a rectangular parallelopiped is 5:3. and its height is 6 cm. If the total surface area of the parallelopiped be 558 sq. cm, then its length in dm is
A9B1.5C10D15 - Question 3 - Select One
Two cubes of sides 6 cm each are kept side by side to form a rectangular parallelopiped. The area (in sq. cm) of the whole suface of the rectangular parallelopiped is
A432B360C396D340
Prove that the shortest distance between the diagonals of a rectangular parallelopiped whose coterminous sides are a, b, c and the edges not meeting it are
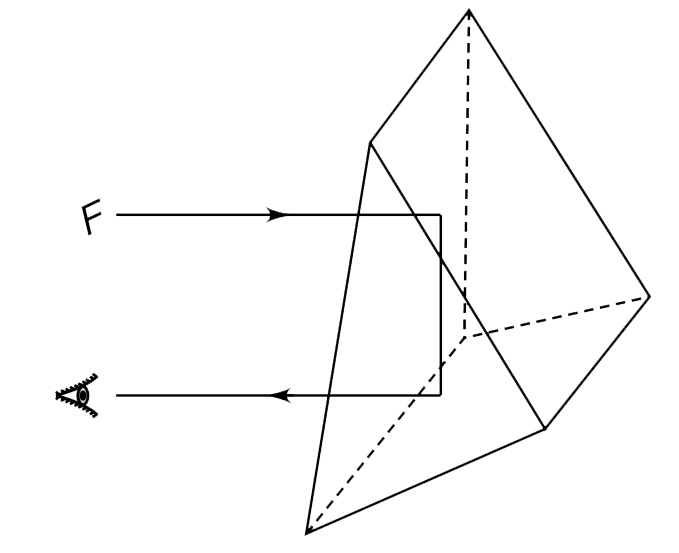
View SolutionLetter F is kept in front of a right triangular psim. The light rays enter perpendicular to the large rectangular face, is reflected twice by small rectangular faces and exits perpendicularly to the large rectangular face (see Fig.). Draw the image of the letter seen by the eye.
 View Solution
View SolutionThe three different face diagonals of a cuboid (rectangular parallelopiped) have lengths 39, 40, 41.The length of the main diagonal of the cuboid which joins a pair of opposite corners :
View SolutionIf two adjacent sides of a rectangular parallelopiped are 1 cm and 2 cm and the total surface area of the parallelopiped is 22 square cm, then the diagonal of the parallelopied is
View SolutionThe volume of the parallelopiped constructed on the diagonals of the faces of the given rectangular parallelopiped is m times the volume of the given parallelopiped. Then m is equal to
View Solution
