If two adjacent sides of a rectangular parallelopiped are 1 cm and 2 cm and the total surface area of the parallelopiped is 22 square cm, then the diagonal of the parallelopied is
4 cm
The correct Answer is:C
To find the diagonal of the rectangular parallelepiped, we will follow these steps:
Step 1: Understand the dimensions
Let the dimensions of the rectangular parallelepiped be:
- Length (l) = 1 cm
- Width (w) = 2 cm
- Height (h) = ?
Step 2: Use the formula for total surface area
The formula for the total surface area (SA) of a rectangular parallelepiped is given by:
SA=2(lw+lh+wh)
Given that the total surface area is 22 cm², we can set up the equation:
2(1⋅2+1⋅h+2⋅h)=22
Step 3: Simplify the equation
Now, simplify the equation:
2(2+h+2h)=22
2(2+3h)=22
Dividing both sides by 2:
2+3h=11
Step 4: Solve for height (h)
Now, isolate h:
3h=11−2
3h=9
h=3 cm
Step 5: Calculate the diagonal
The formula for the diagonal (d) of a rectangular parallelepiped is:
d=√l2+w2+h2
Substituting the values we have:
d=√12+22+32
d=√1+4+9
d=√14
Final Answer
Thus, the diagonal of the rectangular parallelepiped is:
d=√14 cm
---
Let the dimensions of the rectangular parallelepiped be:
- Length (l) = 1 cm
- Width (w) = 2 cm
- Height (h) = ?
The formula for the total surface area (SA) of a rectangular parallelepiped is given by:
SA=2(lw+lh+wh)
Given that the total surface area is 22 cm², we can set up the equation:
2(1⋅2+1⋅h+2⋅h)=22
Now, simplify the equation:
2(2+h+2h)=22
2(2+3h)=22
Dividing both sides by 2:
2+3h=11
Now, isolate h:
3h=11−2
3h=9
h=3 cm
The formula for the diagonal (d) of a rectangular parallelepiped is:
d=√l2+w2+h2
Substituting the values we have:
d=√12+22+32
d=√1+4+9
d=√14
Thus, the diagonal of the rectangular parallelepiped is:
d=√14 cm
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:Test Yourself
Explore 28 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE VI
Explore 47 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm , and the diagonal ac measures 42 cm . Find the area of the parallelogram
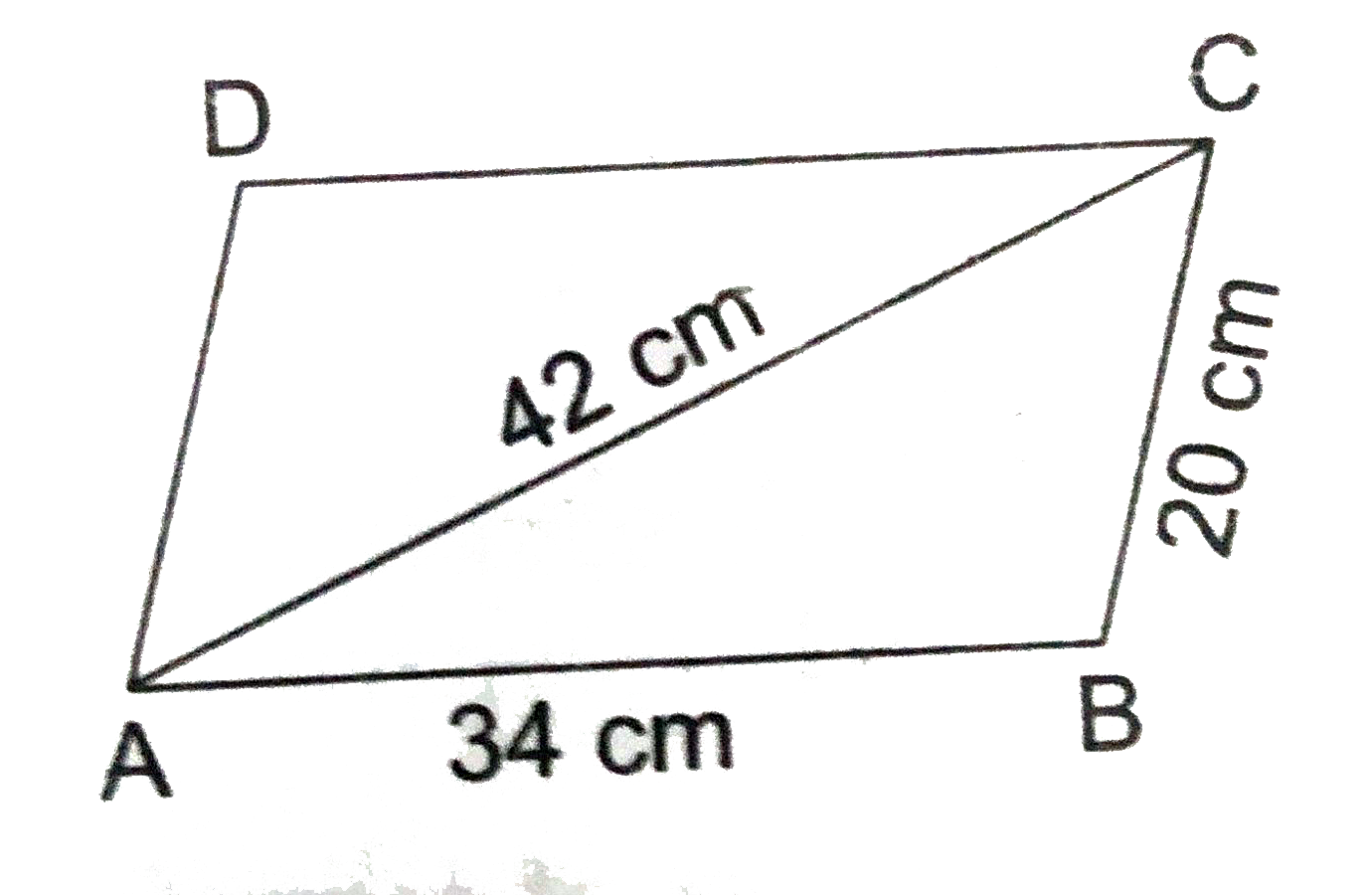
View SolutionThe adjacent sides of a parallelogram ABCD measure 34 cm and20 cm , and the diagonal AC measures 42 cm Find the area of the parallelogram.
View Solution
Knowledge Check
The ratio of the length and breadth of a rectangular parallelopiped is 5:3. and its height is 6 cm. If the total surface area of the parallelopiped be 558 sq. cm, then its length in dm is
A9B1.5C10D15Two adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
A40√3cm2B49√3cm2C48√6cm2D58√6cm2The edges of a rectangular box are in the ratio 1:2:3 and its total surface area is 88cm2 the volume of the box is
A24cm3B48cm3C64cm3D120cm3
The diagonal of a square of side 8 cm is
View SolutionIf the edges of a rectangular parallelopiped are 3, 2, 1 then the angle between a pair of diagonals is given by
View SolutionThe two adjacent sides of parallelogram are 25 cm and 40 cm respectively . The altitude drawn on the longer side is 18 cm, then the area of the parallelogram is :
View SolutionThe two adjacent sides of parallelogram are 25 cm and 40 cm respectively . The altitude drawn on the longer side is 18 cm, then the area of the parallelogram is :
View SolutionTwo adjacent sides of a parallelogram are 21 cms and 20 cms. The diagonal joining the end points of these two sides is 29 cms. The area of the parallelogram (in sq. cms) is
View Solution