The triangles inside △ABC , shown above, are formed by joining the midpoints of the sides and then repeating the process. If a point is chosen at random inside △ABC ,what is the probability that the point lies in the shaded region ?
The correct Answer is:A, D
To solve the problem of finding the probability that a randomly chosen point inside triangle ABC lies in the shaded region (the smallest triangle formed by repeatedly joining the midpoints of the sides), we can follow these steps:
Step 1: Understand the process of forming triangles
We start with triangle ABC. By joining the midpoints of the sides of triangle ABC, we form a new triangle, which we will denote as triangle DEF. This process can be repeated indefinitely, creating smaller triangles within the previous triangles.
Hint: Visualize the process of forming triangles by joining midpoints to better understand the relationships between the areas.
Step 2: Calculate the area of triangle DEF
The area of triangle DEF is one-fourth of the area of triangle ABC. This is because when we join the midpoints of a triangle, the new triangle formed has sides that are half the length of the original triangle's sides. Therefore, the area scales by the square of the ratio of the sides.
Hint: Remember that area scales with the square of the linear dimensions. If the sides are halved, the area is reduced by a factor of (1/2)2=1/4.
Step 3: Calculate the area of triangle HIG
Continuing this process, the area of triangle HIG (formed by joining the midpoints of triangle DEF) will also be one-fourth of the area of triangle DEF. Thus, the area of triangle HIG will be:
Area of HIG=14×Area of DEF=14×14×Area of ABC=116×Area of ABC
Hint: Keep track of how each new triangle's area relates to the previous triangle's area.
Step 4: Calculate the area of triangle PQR
Similarly, the area of triangle PQR (formed by joining the midpoints of triangle HIG) will be:
Area of PQR=14×Area of HIG=14×116×Area of ABC=164×Area of ABC
Hint: You can see a pattern emerging: each new triangle's area is one-fourth of the area of the triangle before it.
Step 5: Determine the probability
The probability that a randomly chosen point inside triangle ABC lies within the shaded region (triangle PQR) is the ratio of the area of triangle PQR to the area of triangle ABC:
Probability=Area of PQRArea of ABC=1/64×Area of ABCArea of ABC=164
Hint: The probability is simply the ratio of the area of the shaded region to the area of the entire triangle.
Final Answer
Thus, the probability that a randomly chosen point inside triangle ABC lies in the shaded region is:
164
We start with triangle ABC. By joining the midpoints of the sides of triangle ABC, we form a new triangle, which we will denote as triangle DEF. This process can be repeated indefinitely, creating smaller triangles within the previous triangles.
The area of triangle DEF is one-fourth of the area of triangle ABC. This is because when we join the midpoints of a triangle, the new triangle formed has sides that are half the length of the original triangle's sides. Therefore, the area scales by the square of the ratio of the sides.
Continuing this process, the area of triangle HIG (formed by joining the midpoints of triangle DEF) will also be one-fourth of the area of triangle DEF. Thus, the area of triangle HIG will be:
Area of HIG=14×Area of DEF=14×14×Area of ABC=116×Area of ABC
Similarly, the area of triangle PQR (formed by joining the midpoints of triangle HIG) will be:
Area of PQR=14×Area of HIG=14×116×Area of ABC=164×Area of ABC
The probability that a randomly chosen point inside triangle ABC lies within the shaded region (triangle PQR) is the ratio of the area of triangle PQR to the area of triangle ABC:
Probability=Area of PQRArea of ABC=1/64×Area of ABCArea of ABC=164
Thus, the probability that a randomly chosen point inside triangle ABC lies in the shaded region is:
164
Topper's Solved these Questions
Similar Questions
In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionThe triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is
View SolutionIn a ABC , find the measures of the angles of the triangle formed by joining the mid-points of the sides of this triangle.
View SolutionIn a ABC , find the measures of the angles of the triangle formed by joining the mid-points of the sides of this triangle.
View SolutionProve that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are congruent to each other.
View SolutionIn the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the larger square, what is the probability that it will be from the small square?
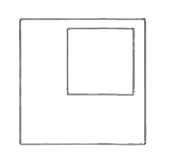
View SolutionIn the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View Solutionprove that the area of a triangle is four times the area of the triangle formed by joining the mid-points of its sides.
View SolutionA side of an equilarteral triangle is 20 cm long .A second equilateral triangle is inscribed in it by joning the mid -point of the sides of the first triangle . The process is caontinued as shown in the accompanying diagram . find the perimeter of the sixth inscribed equilateral triangle .
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View Solution
