The value of xyz is 55 or 34355 according as the series a,x,y,z,b is an AP or HP. Find the values of a and b given that they are positive integers.
To solve the problem, we need to find the values of a and b given that the series a,x,y,z,b can either be in Arithmetic Progression (AP) or Harmonic Progression (HP), and the product xyz is either 55 or 34355.
Step 1: Case 1 - AP
Assuming a,x,y,z,b are in AP, we can express x,y,z in terms of a and b.
1. The common difference d can be expressed as:
d=b−a4
2. Now we can express x,y,z:
- x=a+d=a+b−a4=3a+b4
- y=a+2d=a+2⋅b−a4=a+2b2
- z=a+3d=a+3⋅b−a4=3b+a4
3. The product xyz can be calculated as:
xyz=(3a+b4)(a+2b2)(3b+a4)
Setting this equal to 55:
(3a+b)(a+2b)(3b+a)32=55
This simplifies to:
(3a+b)(a+2b)(3b+a)=1760(Equation 1)
Step 2: Case 2 - HP
Now, assuming a,x,y,z,b are in HP, we can express the reciprocals as being in AP.
1. The common difference f for the reciprocals is:
f=1b−1a⋅14
2. The expressions for x,y,z become:
- x=4ab3b+a
- y=2aba+b
- z=4ab3a+b
3. The product xyz can be calculated as:
xyz=(4ab3b+a)(2aba+b)(4ab3a+b)
Setting this equal to 34355:
32a3b3(3b+a)(a+b)(3a+b)=34355(Equation 2)
Step 3: Solve the Equations
1. Multiply Equation 1 and Equation 2:
(3a+b)(a+2b)(3b+a)⋅32a3b3(3b+a)(a+b)(3a+b)=55⋅34355
Simplifying, we find:
(a+b)3=343
Thus,
a+b=7
2. Now, we have a+b=7 and we can find ab from the earlier product equation.
3. The possible pairs of (a,b) that are positive integers are:
- (1,6)
- (2,5)
- (3,4)
- (4,3)
- (5,2)
- (6,1)
However, we need to check which of these pairs satisfy the product condition from either Equation 1 or Equation 2.
Conclusion
After testing pairs, we find that:
- If a=1, then b=6 or vice versa satisfies the conditions.
Thus, the values of a and b are 1 and 6.
d=b−a4
- x=a+d=a+b−a4=3a+b4
- y=a+2d=a+2⋅b−a4=a+2b2
- z=a+3d=a+3⋅b−a4=3b+a4
xyz=(3a+b4)(a+2b2)(3b+a4)
Setting this equal to 55:
(3a+b)(a+2b)(3b+a)32=55
This simplifies to:
(3a+b)(a+2b)(3b+a)=1760(Equation 1)
f=1b−1a⋅14
- x=4ab3b+a
- y=2aba+b
- z=4ab3a+b
xyz=(4ab3b+a)(2aba+b)(4ab3a+b)
Setting this equal to 34355:
32a3b3(3b+a)(a+b)(3a+b)=34355(Equation 2)
(3a+b)(a+2b)(3b+a)⋅32a3b3(3b+a)(a+b)(3a+b)=55⋅34355
Simplifying, we find:
(a+b)3=343
Thus,
a+b=7
- (1,6)
- (2,5)
- (3,4)
- (4,3)
- (5,2)
- (6,1)
- If a=1, then b=6 or vice versa satisfies the conditions.
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 1
5 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 2
11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
The values of xyz is 152 or 185 according as the series a,x,y,z,b is an AP or HP. Find the values of a&b assuming them to be positive integer.
View SolutionFind the value of x, y and z
View SolutionFind the value of x, y and z
View SolutionFind the value of x,y and z.
View SolutionFind the values of x,y and z in the given figure.
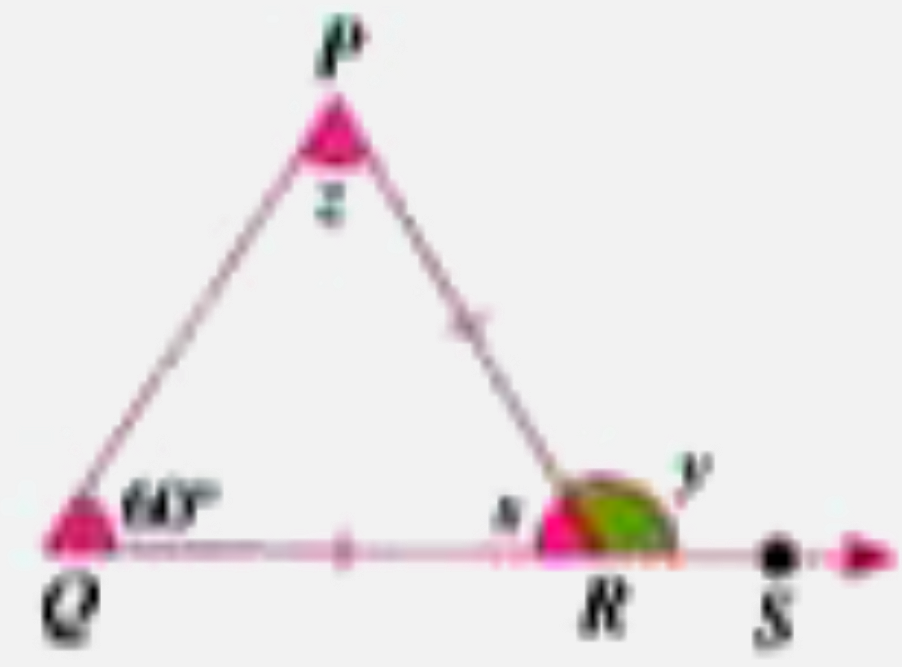
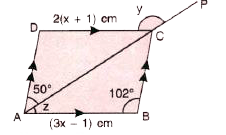
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
View SolutionFind the value of :
x3+y3+3xyz given that x=−1,y=2andz=3
View SolutionIf ax=b,by=c,cz=a, then find the value of xyz.
View SolutionIf ax=b,by=c,cz=a, then find the value of xyz.
View SolutionThe points A(2,9),B(a,5),C(5,5) are the vertices of a triangle ABC right angled at B . Find the value of a and hence the area of ABC.
View Solution
