The vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
Video Solution
Text Solution
The correct Answer is:(−a,a(t1+t2+t3)+at1t2t3)
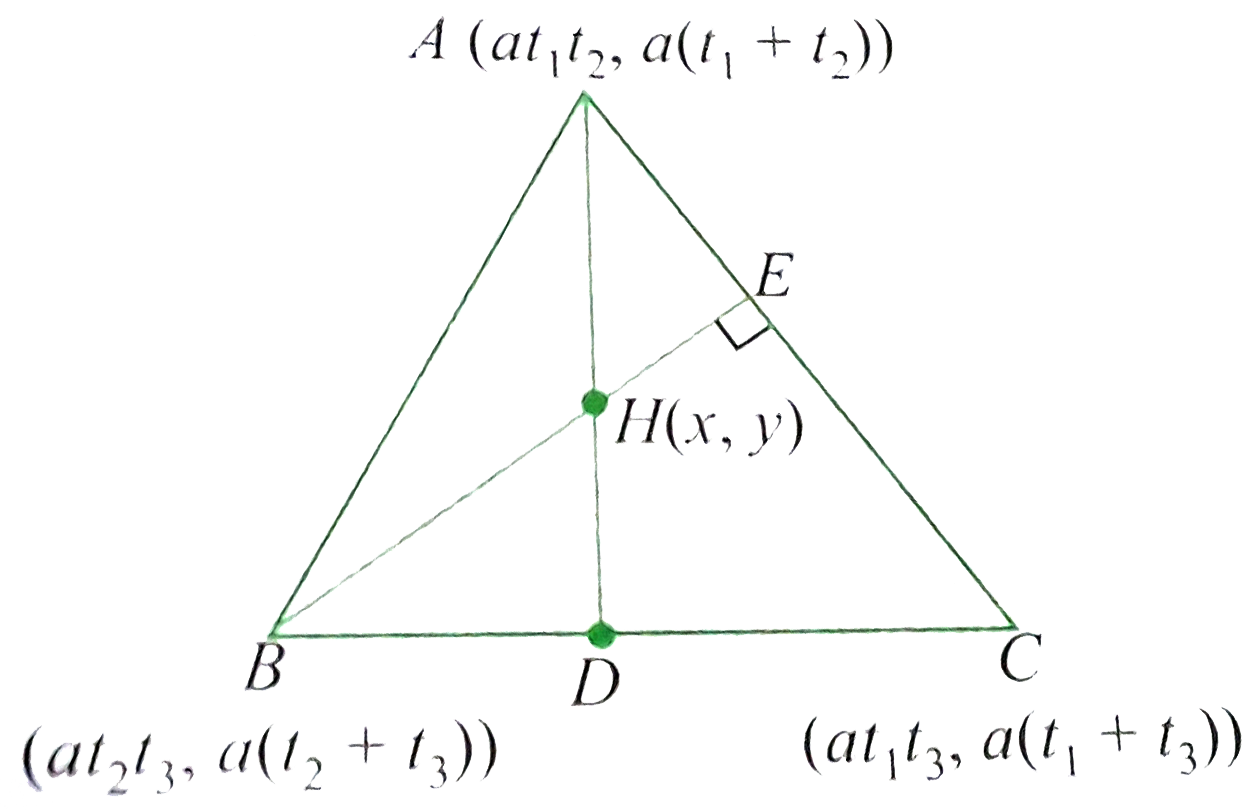
We know that orthocenter of Δ is point of concurrencyof altitudes. Let orthocenter be H(x,y).
Now, slope of BC=(t1+t3)−a(t2+t3)at1t3−at2t3
BC=(t1+t3−t2−t3)at1(t1−t2)=1t3
∴ Slope ofAD=−t3
Also, slope of AD=Slope of AH=y−(t1+t2)x−at1t2=−t3
or xt3=at1t2t3+a(t1+t2)
Similarly , by symmetry form AC⊥BE, we get (1)
xt1+y=at1t2t3+a(t2_t3) (2)
Solving (1) and (2),we get
x=−a,y=a(t1+t2+t3_+at1t2t3
∴ Orthocenter is H(−a,a(t1+t2+t3)+at1t2t3)
|
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.4
8 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.5
5 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Knowledge Check
If t1,t2 and t3 are distinct, then the points (t1,2at1+at31),(t2,2at2+at32) and (t3,2at3+at33) are collinear, when
At1t2t3=1Bt1+t2+t3=t1t2t3Ct1+t2+t3=0Dt1+t2+t3=1
The vertices of a triangle are
[at1t2,a(t1+t2)],[at2t3,a(t2+t3)]
[at3t1,a(t3+t1)]
Find the coordinates of its orthocentre.
View SolutionIf the orthocentre of the triangle formed by the points t1,t2,t3 on the parabola y2=4ax is the focus, the value of |t1t2+t2t3+t3t1| is
View SolutionProve that the area of the triangle whose vertices are :
(at21,2at1), (at22,2at2), (at23,2at3) is a2(t1−t2)(t2−t3)(t3−t1).
View SolutionFind the are of triangle whose vertex are: (at1,at1)(at2,at2)(at3,at3)
View SolutionIf 3(t−3)=5(2t+1), then t=?
View SolutionProve that the area of the triangle whose vertices are (t,t−2),(t+2,t+2)and(t+3,t) is independent of t.
View SolutionProve that the area of the triangle whose vertices are (t,t−2),(t+2,t+2), and (t+3,t) is independent of t.
View Solution
