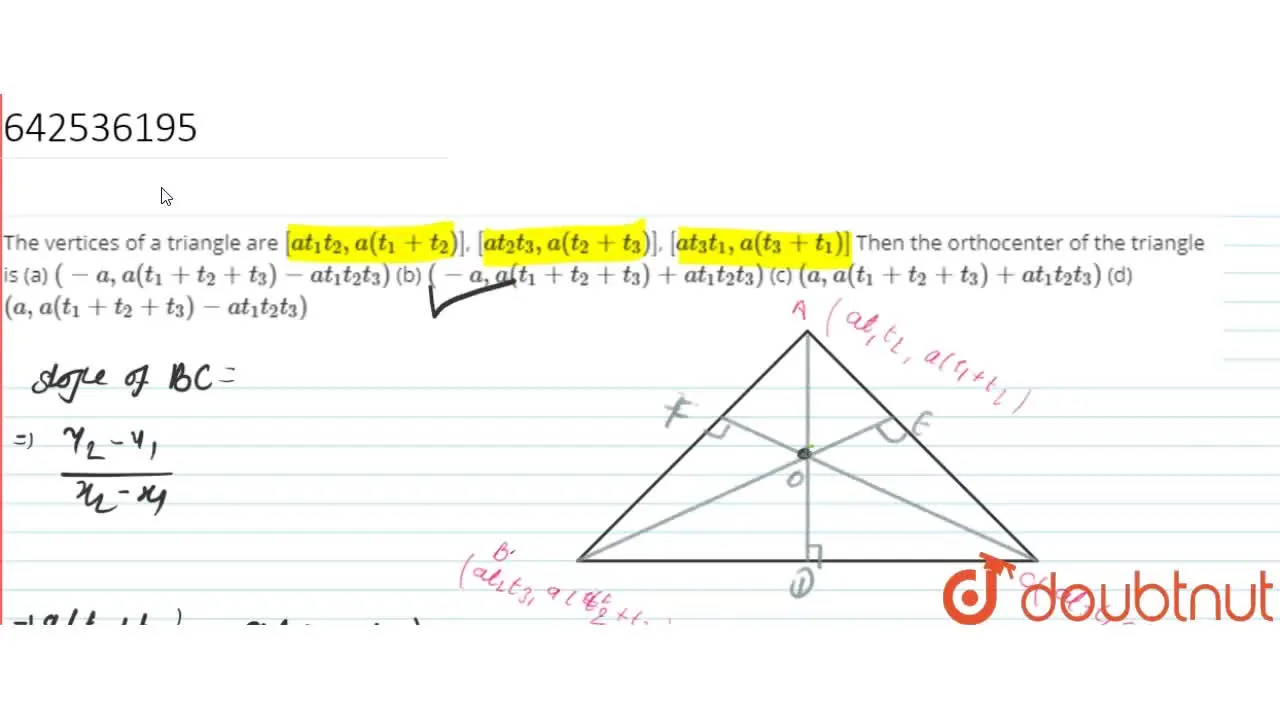
The vertices of a triangle are $[a t_{1} t_{2}, a (t_{1} + t_{2})]$ , $[a t_{2} t_{3}, a (t_{2} + t_{3})]$ , $[a t_{3} t_{1}, a (t_{3} + t_{1})]$ Then the orthocenter of the triangle is (a) $(- a, a (t_{1} + t_{2} + t_{3}) - a t_{1} t_{2} t_{3})$ (b) $(- a, a (t_{1} + t_{2} + t_{3}) + a t_{1} t_{2} t_{3})$ (c) $(a, a (t_{1} + t_{2} + t_{3}) + a t_{1} t_{2} t_{3})$ (d) $(a, a (t_{1} + t_{2} + t_{3}) - a t_{1} t_{2} t_{3})$

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the orthocenter of the triangle with vertices given by the coordinates $(a t_{1} t_{2}, a (t_{1} + t_{2}))$ , $(a t_{2} t_{3}, a (t_{2} + t_{3}))$ , and $(a t_{3} t_{1}, a (t_{3} + t_{1}))$ , we will follow these steps:
Step 1: Identify the vertices
Let the vertices of the triangle be:
- $A = (a t_{1} t_{2}, a (t_{1} + t_{2}))$
- $B = (a t_{2} t_{3}, a (t_{2} + t_{3}))$
- $C = (a t_{3} t_{1}, a (t_{3} + t_{1}))$
Step 2: Calculate the slopes of the sides
We will calculate the slopes of sides $B C$ and $A C$ .
Slope of $B C$
Using the formula for the slope $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ :
$slope of B C = \frac{a (t_{2} + t_{3}) - a (t_{3} + t_{1})}{a t_{2} t_{3} - a t_{3} t_{1}} = \frac{a (t_{2} - t_{1})}{a (t_{2} t_{3} - t_{3} t_{1})} = \frac{t_{2} - t_{1}}{t_{2} t_{3} - t_{3} t_{1}}$
Slope of $A C$
$slope of A C = \frac{a (t_{1} + t_{2}) - a (t_{3} + t_{1})}{a t_{1} t_{2} - a t_{3} t_{1}} = \frac{a (t_{2} - t_{3})}{a (t_{1} t_{2} - t_{3} t_{1})} = \frac{t_{2} - t_{3}}{t_{1} t_{2} - t_{3} t_{1}}$
Step 3: Find the slopes of the altitudes
The slopes of the altitudes are the negative reciprocals of the slopes of the sides.
Slope of altitude from $A$ (perpendicular to $B C$ )
$slope of altitude from A = - \frac{t_{2} t_{3} - t_{3} t_{1}}{t_{2} - t_{1}}$
Slope of altitude from $B$ (perpendicular to $A C$ )
$slope of altitude from B = - \frac{t_{1} t_{2} - t_{3} t_{1}}{t_{2} - t_{3}}$
Step 4: Set up equations for the altitudes
Using point-slope form $y - y_{1} = m (x - x_{1})$ , we can write the equations of the altitudes.
Equation of altitude from $A$
$y - a (t_{1} + t_{2}) = - \frac{t_{2} t_{3} - t_{3} t_{1}}{t_{2} - t_{1}} (x - a t_{1} t_{2})$
Equation of altitude from $B$
$y - a (t_{2} + t_{3}) = - \frac{t_{1} t_{2} - t_{3} t_{1}}{t_{2} - t_{3}} (x - a t_{2} t_{3})$
Step 5: Solve the equations simultaneously
To find the orthocenter, we need to solve the two equations simultaneously. This will yield the coordinates of the orthocenter $(x, y)$ .
After solving these equations, we find:
$x = - a$
$y = a (t_{1} + t_{2} + t_{3} + t_{1} t_{2} t_{3})$
Conclusion
Thus, the orthocenter of the triangle is:
$(- a, a (t_{1} + t_{2} + t_{3} + t_{1} t_{2} t_{3}))$

Updated on:18/9/2024

|

Class 11 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CONIC SECTIONS-All Questions

Home
Ask Doubt
Profile