The width of each of five continuous classes in a frequency distribution is 5 and the lower class limit of the lowest class is 10. The upper class limit of the highest class is
15
25
35
40
The correct Answer is:C
Let x and y be the upper and lower class limit of frequency distribution.
Given, width of the class =5
⇒x−y=5 ……….(i)
Also, given lower class (y)=10
On putting y=10 in Eq. (i), we get
x−10=5⇒x=15
So, the upper class limit of the lowest class is 15.
Hence, the upper limit of the highest class
= (Number of continuous classes x Class with + Lower class limit of the lowest class)
=5×5+10=25+10=35
Hence, the upper class limit of the highest class is 35.
Alternate method
After finding the upper class limit of the lowest class, the five continuous classes in a frequency distribution with width 5 are 10-15, 15-20, 20-25, 25-30, and 30-35.
Thus, the highest class is 30-35,
Hence, the upper limit of the class is 35.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLARCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLARCHAPTER - QUADRILATERALS EXERCISE - Quadrilaterals
56 Videos
- TRIANGLESBOOK - NCERT EXEMPLARCHAPTER - TRIANGLESEXERCISE - Triangles
55 Videos
Similar Questions
(i)Find the class mark of the class 90-120.
(ii)In a frequency distribution, the mid-value of the class is 10 and width of the class is 6. Find the lowe limit of the class.
(iii)The width of each of the five continuous classes in a frequency distribution is 5 and lowe class limit of the lowest class is 10. What is the upper class limit of the highest class?
(iv) The class marks of a frequency distribution are 15,20,25...... Find the class corresponding to the class mark 20.
(v)In the class intervals 10-20, 20-30, find the class in which 20 is included.
View SolutionThe width of each of nine classes in a frequency distribution is 2.5 and the lower class boundary of the lowest class 10.6. Then the upper class boundary of the highest class is 35.6 (b) 33.1 (c) 30.6 (d) 28.1
View Solution
Knowledge Check
The width of each of the five continuous classes in a frequency distribution is 5 and the upper class limit of the last class is 60. The lower class limit of the lowest class is
A45B25C35D40Find the lower limit of the median class
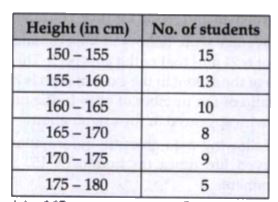 A165B155C160D170
A165B155C160D170In a frequency distribution, the mid-value of a class is 10 and width of each class is 6. The upper limit of the class is
A13B7C8D12
If the width of each of the ten classes in frequency distribution is 2.5 and the lower class boundary of the lowest class is 5.1, then the upper class boundary of the highest class IS
View SolutionWrite the upper classs limit and the lower class limit of the class 35-40.
View SolutionIn a frequency distribution, the mid values of a class is 10 and width of the class is 6. The lower limit of the class is
View SolutionIn a frequency distribution, the mid value of a class is 10 and the width of the class is 6. The lower limit of the class is
View SolutionFor the following distribution

the lower limits of the modal class is
View Solution
