There are exactly two distinct linear functions, which map [-1,1] onto [0,3]. Find the point of intersection of the two functions.
The correct Answer is:x=0 and y=32
To solve the problem, we need to find the point of intersection of two distinct linear functions that map the interval (−1,1) onto (0,3).
1. Understanding the Functions:
We are looking for two linear functions of the form f(x)=ax+b that map the interval (−1,1) to (0,3). This means:
- f(−1)=0
- f(1)=3
2. Setting Up the Equations:
For the first function, we can set up the equations based on the mappings:
- From f(−1)=0:
−a+b=0(Equation 1)
- From f(1)=3:
a+b=3(Equation 2)
3. Solving the Equations:
Now we can solve these two equations simultaneously.
- From Equation 1, we can express b in terms of a:
b=a(Substituting into Equation 2)
- Substitute b=a into Equation 2:
a+a=3⟹2a=3⟹a=32
- Substitute a back into Equation 1 to find b:
b=32
4. First Function:
Thus, the first linear function is:
f1(x)=32x+32
5. Finding the Second Function:
For the second function, we can switch the mappings:
- Let f(−1)=3 and f(1)=0:
- From f(−1)=3:
−a+b=3(Equation 3)
- From f(1)=0:
a+b=0(Equation 4)
6. Solving the Second Set of Equations:
- From Equation 4, express b in terms of a:
b=−a(Substituting into Equation 3)
- Substitute b=−a into Equation 3:
−a−a=3⟹−2a=3⟹a=−32
- Substitute a back into Equation 4 to find b:
b=32
7. Second Function:
Thus, the second linear function is:
f2(x)=−32x+32
8. Finding the Point of Intersection:
To find the point of intersection of f1(x) and f2(x), set them equal to each other:
32x+32=−32x+32
- Rearranging gives:
32x+32x=0⟹3x=0⟹x=0
- Substitute x=0 into either function to find y:
f1(0)=32(0)+32=32
9. Final Answer:
The point of intersection of the two functions is:
(0,32)
We are looking for two linear functions of the form f(x)=ax+b that map the interval (−1,1) to (0,3). This means:
- f(−1)=0
- f(1)=3
For the first function, we can set up the equations based on the mappings:
- From f(−1)=0:
−a+b=0(Equation 1)
- From f(1)=3:
a+b=3(Equation 2)
Now we can solve these two equations simultaneously.
- From Equation 1, we can express b in terms of a:
b=a(Substituting into Equation 2)
- Substitute b=a into Equation 2:
a+a=3⟹2a=3⟹a=32
- Substitute a back into Equation 1 to find b:
b=32
Thus, the first linear function is:
f1(x)=32x+32
For the second function, we can switch the mappings:
- Let f(−1)=3 and f(1)=0:
- From f(−1)=3:
−a+b=3(Equation 3)
- From f(1)=0:
a+b=0(Equation 4)
- From Equation 4, express b in terms of a:
b=−a(Substituting into Equation 3)
- Substitute b=−a into Equation 3:
−a−a=3⟹−2a=3⟹a=−32
- Substitute a back into Equation 4 to find b:
b=32
Thus, the second linear function is:
f2(x)=−32x+32
To find the point of intersection of f1(x) and f2(x), set them equal to each other:
32x+32=−32x+32
- Rearranging gives:
32x+32x=0⟹3x=0⟹x=0
- Substitute x=0 into either function to find y:
f1(0)=32(0)+32=32
The point of intersection of the two functions is:
(0,32)
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 9
10 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 10
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 7
5 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
There are exactly two distinct linear functions, ______ and ______, which map [-1,1] onto [0,2].
View SolutionLet f(x) be a linear function which maps [-1, 1] onto [0, 2], then f(x) can be
View SolutionFind the points of discontinuity of the function: f(x)=12sinx−1
View SolutionIf fandg are two distinct linear functions defined on R such that they map {−1,1] onto [0,2] and h:R−{−1,0,1}→R defined by h(x)=f(x)g(x), then show that ∣∣∣h(h(x))+h(h(1x))∣∣∣>2.
View SolutionIf there are only two linear functions f and g which map [1,2]on[4,6] and in a ΔABC,c=f(1)+g(1) and a is the maximum valur of r2, where r is the distance of a variable point on the curve x2+y2−xy=10 from the origin, then sin A: sin C is
View SolutionIn how many points two distinct lines can intersect?
View SolutionIn how many points two distinct planes can intersect?
View SolutionFind the orthocentre of the triangle whose angular points are (0, 0), (2, -1), (-1, 3).
[Note. Orthocentre is the point of intersection of the altitudes]
View SolutionThe distinct linear functions which map [-1, 1] onto [0, 2] are f(x)=x+1, g(x)=−x+1 (b) f(x)=x−1, g(x)=x+1 (c) f(x)=−x−1, g(x)=x−1 (d) none of these
View Solution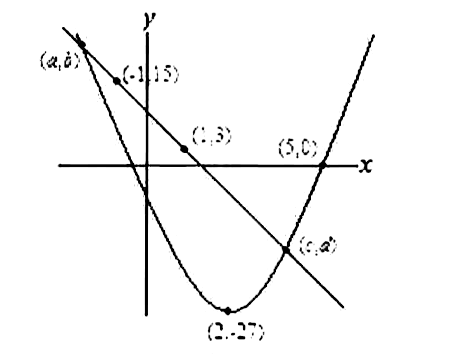
The xy-plane above shows the two points of intersection of the graphs of a linear function and a quadratic function. The leftmost point of intersection has coordinates (a,b) and the rightmost point of intersection has coordinates (c,d) . If the vertex of the graph of the quadratic function is at (2, -27) , what is the value of b−d ?
View Solution
