Question

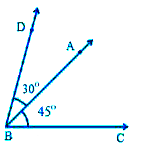
There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?

Explanation

To solve the question about the measures of the angles formed at the corners of the two set-squares and to find out if they have any common angle measures, we can follow these steps:

1. Identify the Angles of the First Set Square:
- The first set square has angles measuring 90 degrees, 45 degrees, and 45 degrees.
- Therefore, the angles are: 90°, 45°, 45°.

2. Identify the Angles of the Second Set Square:
- The second set square has angles measuring 90 degrees, 30 degrees, and 60 degrees.
- Therefore, the angles are: 90°, 30°, 60°.

3. List the Angles from Both Set Squares:
- From the first set square: 90°, 45°, 45°.
- From the second set square: 90°, 30°, 60°.

4. Determine Common Angles:
- Now, we will compare the angles from both set squares to find any common angles.
- The common angle between the two set squares is 90°.

5. Conclusion:
- The angles formed at the corners of the two set squares are 90°, 45°, 45° for the first set square and 90°, 30°, 60° for the second set square.
- The common angle measure between the two set squares is 90°.

Summary:
- First Set Square Angles: 90°, 45°, 45°
- Second Set Square Angles: 90°, 30°, 60°
- Common Angle: 90°