Three coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
Video Solution
Text Solution
Let the length of an edge of the cube be taken as unity and the vectors represented by OA, OB and OC (let the three coterminous edges of unit be ˆi,ˆjandˆk, respectively). OR, OS and OT are the three diagonals of the three adjacent faces of the cube along which act the forces of magnitudes a,2aand3a, respectively. To find the vectors representing these forces, we will first find unit vectors in these directions and then multiply them by the corresponding given magnitudes of these forces.
Since −−→OR=ˆj+ˆk, the unit vector along OR is 1√2(ˆj+ˆk).

Hence, force −→F1 of magnitude a along OR is given by
−→F1=a√2(ˆi+ˆk)
Similarly, force −→F1 of magnitude 2a along OS is 2a√2(ˆk+ˆi) and force −→F3 of magnitude 3a along OT is 3a√2(ˆi+ˆj).
If →R is their resultant, then
→R=−→F1+−→F2+−→F3
=a√2(ˆj+ˆk)+2a√2(ˆk+ˆi)+3a√2(ˆi+ˆj)
=5a√2ˆi+4a√2ˆj+3a√2ˆk
Again, −−→OR+−−→OS+−−→OT=ˆj+ˆk+ˆi+ˆk+ˆi+ˆj
=2(ˆi+ˆj+ˆk)
Also, −−→OP=−−→OT+−−→TP=(ˆi+ˆj+ˆk) (∵−−→OT=ˆi+ˆjand−−→TP=−−→OC=ˆk)
−−→OR+−−→OS+−−→OT=2−−→OP
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise 1.120videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise 1.27videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises324videos
INTEGRALS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank24videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum of the three vectors determined by the medians of triangle directed from the vertices is
A0B1C−1D13 - Question 2 - Select One
Three forces of magnitudes 1,2, and 3 dynes meet in a point and act along diagonals of three adjacent faces of a cube.The resultant force is
A114 dyneB6 dynesC5 dynesDnone of the abive - Question 3 - Select One
Three forces of magnitudes 1,2, and 3 dynes meet in a point and act along diagonals of three adjacent faces of a cube.The resultant force is
A114 dyneB6 dynesC5 dynesDnone of the abive
Prove that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionThe areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V2=xyz.
View SolutionThe areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V2=xyz.
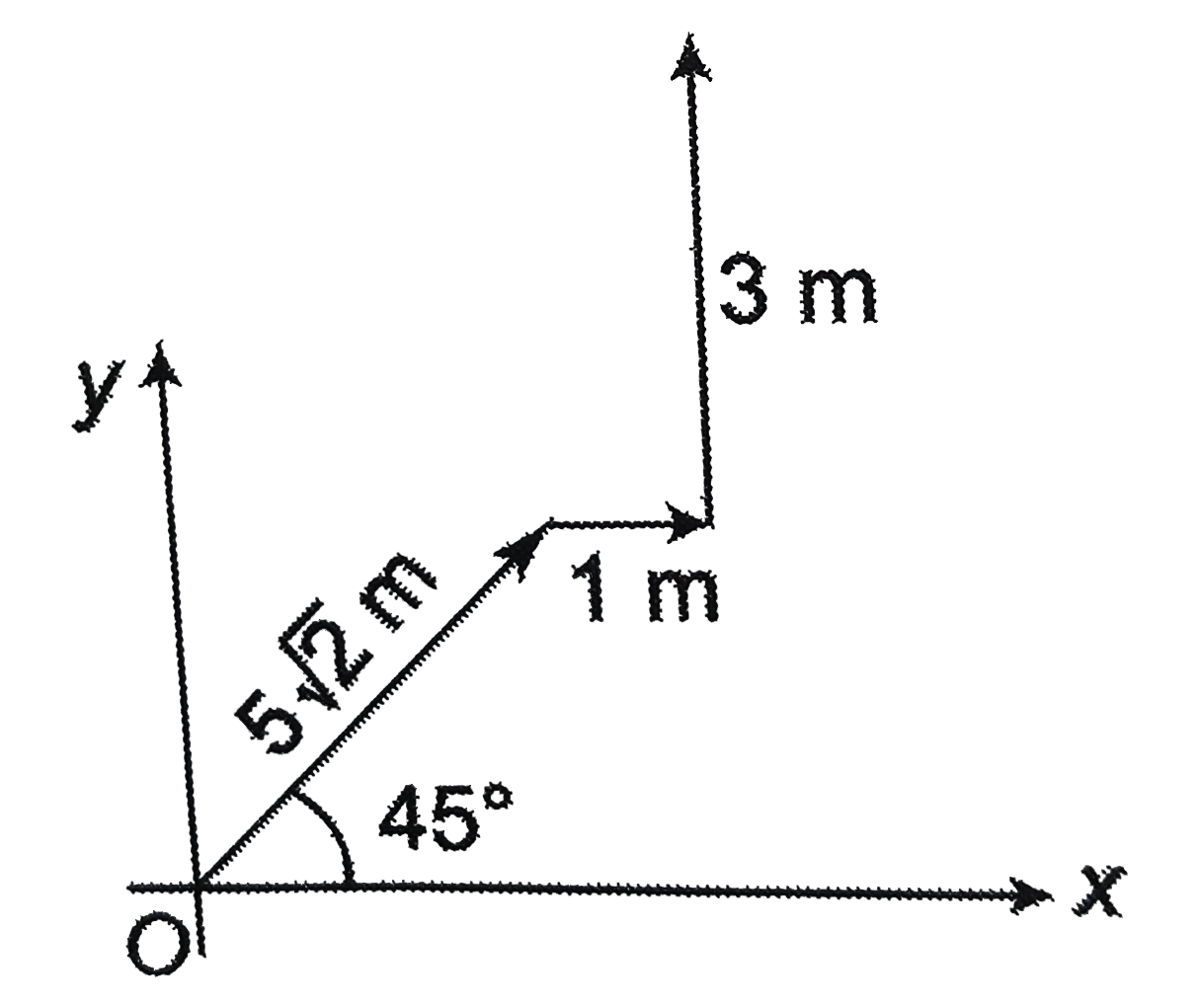
View SolutionFind the resultant of three vectors shown in the figure.
 View Solution
View Solution